解:(1)设圆心坐标为(m,n)(m<0,n>0),
则该圆的方程为(x-m)
2+(y-n)
2=8已知该圆与直线y=x相切,
那么圆心到该直线的距离等于圆的半径,则

=2

即|m-n|=4…①
又圆与直线切于原点,将点(0,0)代入得m
2+n
2=8…②
联立方程①和②组成方程组解得
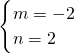
故圆的方程为(x+2)
2+(y-2)
2=8;
(2)∵椭圆

+

=1与圆C的一个交点到椭圆两焦点的距离之和为10.
∴2a=10,得a=5,a
2=25,
由此可得,椭圆的方程为

+

=1
其焦距c=

=4,右焦点为(4,0),那么|OF|=4.
将两圆的方程联列,得
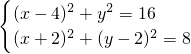
,解之得x=

,y=

.
即存在异于原点的点Q(

,

),
使得该点到右焦点F的距离等于|OF|的长.
分析:(1)设出圆心C(m,n),根据直线y=x与圆相切建立关于m、n的一个方程,而原点在圆C上建立关于m、n的另一个方程,两方程联解即可得到m=-2且n=2,由此即可得到圆C的标准方程;
(2)根据椭圆与圆C的一个交点到椭圆两焦点的距离之和为10,算出a
2=25,从而得到右焦点F(4,0),因此可得以F为圆心半径r=0F=4的圆方程为(x-4)
2+y
2=16,将此方程与圆C方程联解,可得x=

且y=

,所以存在异于原点的点Q(

,

),使得该点到右焦点F的距离等于|OF|的长.
点评:本题给出满足条件的圆C,求圆C的标准方程,并依此探索椭圆

+

=1右焦点F到圆C上一点的距离能否等于4.着重考查了椭圆的标准方程与简单几何性质、圆与圆的位置关系和圆锥曲线的综合等知识,属于中档题.

 的圆C与直线y=x相切于坐标原点O.椭圆
的圆C与直线y=x相切于坐标原点O.椭圆 +
+ =1与圆C的一个交点到椭圆两焦点的距离之和为10.
=1与圆C的一个交点到椭圆两焦点的距离之和为10. =2
=2
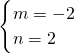
 +
+ =1与圆C的一个交点到椭圆两焦点的距离之和为10.
=1与圆C的一个交点到椭圆两焦点的距离之和为10. +
+ =1
=1 =4,右焦点为(4,0),那么|OF|=4.
=4,右焦点为(4,0),那么|OF|=4.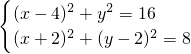 ,解之得x=
,解之得x= ,y=
,y= .
. ,
, ),
), 且y=
且y= ,所以存在异于原点的点Q(
,所以存在异于原点的点Q( ,
, ),使得该点到右焦点F的距离等于|OF|的长.
),使得该点到右焦点F的距离等于|OF|的长. +
+ =1右焦点F到圆C上一点的距离能否等于4.着重考查了椭圆的标准方程与简单几何性质、圆与圆的位置关系和圆锥曲线的综合等知识,属于中档题.
=1右焦点F到圆C上一点的距离能否等于4.着重考查了椭圆的标准方程与简单几何性质、圆与圆的位置关系和圆锥曲线的综合等知识,属于中档题. 

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案