
【题目】关于函数![]() ,
,![]() .有下列命题:
.有下列命题:
①对![]() ,恒有
,恒有![]() 成立.
成立.
②![]() ,使得
,使得![]() 成立.
成立.
③“若![]() ,则有
,则有![]() 且
且![]() .”的否命题.
.”的否命题.
④“若![]() 且
且![]() ,则有
,则有![]() .”的逆否命题.
.”的逆否命题.
其中,真命题有_____________.(只需填序号)
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的普通方程为
的普通方程为![]() ,曲线
,曲线![]() 参数方程为
参数方程为![]() (
(![]() 为参数);以坐标原点
为参数);以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,
,![]() .
.
(1)求![]() 的参数方程和
的参数方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)已知![]() 是
是![]() 上参数
上参数![]() 对应的点,
对应的点,![]() 为
为![]() 上的点,求
上的点,求![]() 中点
中点![]() 到直线
到直线![]() 的距离取得最小值时,点
的距离取得最小值时,点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经过多年的努力,炎陵黄桃在国内乃至国际上逐渐打开了销路,成为炎陵部分农民脱贫致富的好产品.为了更好地销售,现从某村的黄桃树上随机摘下了100个黄桃进行测重,其质量分布在区间![]() 内(单位:克),统计质量的数据作出其频率分布直方图如图所示:
内(单位:克),统计质量的数据作出其频率分布直方图如图所示:
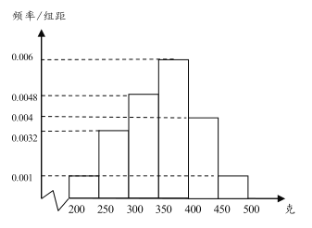
(1)按分层抽样的方法从质量落在![]() ,
,![]() 的黄桃中随机抽取5个,再从这5个黄桃中随机抽2个,求这2个黄桃质量至少有一个不小于400克的概率;
的黄桃中随机抽取5个,再从这5个黄桃中随机抽2个,求这2个黄桃质量至少有一个不小于400克的概率;
(2)以各组数据的中间数值代表这组数据的平均水平,以频率代表概率,已知该村的黄桃树上大约还有100000个黄桃待出售,某电商提出两种收购方案:
A.所有黄桃均以20元/千克收购;
B.低于350克的黄桃以5元/个收购,高于或等于350克的以9元/个收购.
请你通过计算为该村选择收益最好的方案.
(参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司培训员工某项技能,培训有如下两种方式:
方式一:周一到周五每天培训1小时,周日测试
方式二:周六一天培训4小时,周日测试
公司有多个班组,每个班组60人,现任选两组![]() 记为甲组、乙组
记为甲组、乙组![]() 先培训;甲组选方式一,乙组选方式二,并记录每周培训后测试达标的人数如表:
先培训;甲组选方式一,乙组选方式二,并记录每周培训后测试达标的人数如表:
第一周 | 第二周 | 第三周 | 第四周 | |
甲组 | 20 | 25 | 10 | 5 |
乙组 | 8 | 16 | 20 | 16 |
![]() 用方式一与方式二进行培训,分别估计员工受训的平均时间
用方式一与方式二进行培训,分别估计员工受训的平均时间![]() 精确到
精确到![]() ,并据此判断哪种培训方式效率更高?
,并据此判断哪种培训方式效率更高?
![]() 在甲乙两组中,从第三周培训后达标的员工中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求这2人中至少有1人来自甲组的概率.
在甲乙两组中,从第三周培训后达标的员工中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求这2人中至少有1人来自甲组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是某地一家超市在2018年一月份某一周内周2到周6的时间![]() 与每天获得的利润
与每天获得的利润![]() (单位:万元)的有关数据.
(单位:万元)的有关数据.
星期 | 星期2 | 星期3 | 星期4 | 星期5 | 星期6 |
利润 | 2 | 3 | 5 | 6 | 9 |
(1)根据上表提供的数据,用最小二乘法求线性回归直线方程![]() ;
;
(2)估计星期日获得的利润为多少万元.
参考公式: 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sinx-xcosx-x,f′(x)为f(x)的导数.
(1)证明:f′(x)在区间(0,π)存在唯一零点;
(2)若x∈[0,π]时,f(x)≥ax,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com