
【题目】在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴,建立极坐标系.已知曲线C1: ![]() (t为参数),C2:
(t为参数),C2: ![]() (θ为参数). (Ⅰ)化C1 , C2的方程为普通方程,并说明它们分别表示什么曲线;
(θ为参数). (Ⅰ)化C1 , C2的方程为普通方程,并说明它们分别表示什么曲线;
(Ⅱ)若C1上的点P对应的参数为t=﹣ ![]() ,Q为C2上的动点,求线段PQ的中点M到直线C3:ρcosθ﹣
,Q为C2上的动点,求线段PQ的中点M到直线C3:ρcosθ﹣ ![]() ρsinθ=8+2
ρsinθ=8+2 ![]() 距离的最小值.
距离的最小值.
【答案】解:(Ⅰ)∵曲线C1: ![]() (t为参数), ∴曲线C1的普通方程为:(x﹣4)2+(y+3)2=1,
(t为参数), ∴曲线C1的普通方程为:(x﹣4)2+(y+3)2=1,
∵曲线C2: ![]() (θ为参数),
(θ为参数),
∴曲线C2的普通方程为: ![]() ,
,
曲线C1为圆心是(4,﹣3),半径是1的圆.
曲线C2为中心在坐标原点,焦点在x轴上,长半轴长是6,短半轴长是2的椭圆.
(Ⅱ)当t= ![]() 时,P(4,﹣4),
时,P(4,﹣4),
设Q(6cosθ,2sinθ),则M(2+3cosθ,﹣2+sinθ),
∵直线C3:ρcosθ﹣ ![]() ,
,
∴直线C3的直角坐标方程为: ![]() ﹣(8+2
﹣(8+2 ![]() )=0,
)=0,
M到C3的距离d= 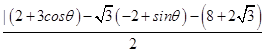
= 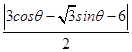
= 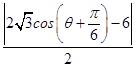
=3﹣ ![]() .
.
从而当cos( ![]() )=1时,d取得最小值3﹣
)=1时,d取得最小值3﹣ ![]()
【解析】(Ⅰ)由cos2θ+sin2θ=1,能求出曲线C1 , C2的普通方程,并能说明它们分别表示什么曲线.(Ⅱ)当t= ![]() 时,P(4,﹣4),设Q(6cosθ,2sinθ),则M(2+3cosθ,﹣2+sinθ),直线C3的直角坐标方程为:
时,P(4,﹣4),设Q(6cosθ,2sinθ),则M(2+3cosθ,﹣2+sinθ),直线C3的直角坐标方程为: ![]() ﹣(8+2
﹣(8+2 ![]() )=0,由此能求出线段PQ的中点M到直线C3:ρcosθ﹣
)=0,由此能求出线段PQ的中点M到直线C3:ρcosθ﹣ ![]() 距离的最小值.
距离的最小值.


科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn,数列{Sn}的前n项和为Tn,满足Tn=2Sn-n2,n∈N*.
(1)求a1的值;
(2)求数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的焦距为2
=1(a>b>0)的焦距为2 ![]() ,椭圆C上任意一点到椭圆两个焦点的距离之和为6. (Ⅰ)求椭圆C的方程;
,椭圆C上任意一点到椭圆两个焦点的距离之和为6. (Ⅰ)求椭圆C的方程;
(Ⅱ)设直线l:y=kx﹣2与椭圆C交于A,B两点,点P(0,1),且|PA|=|PB|,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x)=xlnx有如下结论: ①该函数为偶函数;
②若f′(x0)=2,则x0=e;
③其单调递增区间是[ ![]() ,+∞);
,+∞);
④值域是[ ![]() ,+∞);
,+∞);
⑤该函数的图象与直线y=﹣ ![]() 有且只有一个公共点.(本题中e是自然对数的底数)
有且只有一个公共点.(本题中e是自然对数的底数)
其中正确的是(请把正确结论的序号填在横线上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,三棱锥V﹣ABC中,VA=VB=AC=BC=2,AB=2 ![]() ,VC=1,线段AB的中点为D.
,VC=1,线段AB的中点为D.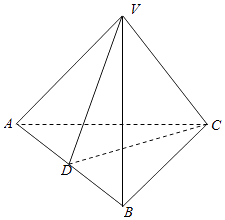
(1)求证:平面VCD⊥平面ABC;
(2)求三棱锥V﹣ABC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设Sn为数列{an}的前n项和,Sn=2n2+5n.
(1)求证:数列{3 ![]() }为等比数列;
}为等比数列;
(2)设bn=2Sn﹣3n,求数列{ ![]() }的前n项和Tn .
}的前n项和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com