
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(Ⅰ)求椭圆![]() 的方程.
的方程.
(Ⅱ)若![]() ,
, ![]() 是椭圆
是椭圆![]() 上两个不同的动点,且使
上两个不同的动点,且使![]() 的角平分线垂直于
的角平分线垂直于![]() 轴,试判断直线
轴,试判断直线![]() 的斜率是否为定值?若是,求出该值;若不是,说明理由.
的斜率是否为定值?若是,求出该值;若不是,说明理由.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(I)由离心率可得![]() 关系,再将点
关系,再将点![]() 坐标代入,可得
坐标代入,可得![]() 间关系,又
间关系,又![]() ,解方程可得
,解方程可得![]() 的值;(II)由
的值;(II)由![]() 的角平分线总垂直于
的角平分线总垂直于![]() 轴,可判断直线
轴,可判断直线![]() 的斜率互为相反数,由两直线都过
的斜率互为相反数,由两直线都过![]() 点,由点斜式可写出直线方程.一一与椭圆方程联立,消去
点,由点斜式可写出直线方程.一一与椭圆方程联立,消去![]() 的值,可得一元二次方程,又
的值,可得一元二次方程,又![]() 点满足条件,可求得
点满足条件,可求得![]() 点的坐标,用
点的坐标,用![]() 表示.再由斜率公式可得直线
表示.再由斜率公式可得直线![]() 的斜率为定值.
的斜率为定值.
试题解析:
(Ⅰ) 因为椭圆![]() 的离心率为
的离心率为![]() , 且过点
, 且过点![]() ,
,
所以![]() ,
, ![]() .
.
因为![]() ,
,
解得![]() ,
, ![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)法1:因为![]() 的角平分线总垂直于
的角平分线总垂直于![]() 轴, 所以
轴, 所以![]() 与
与![]() 所在直线关于直线
所在直线关于直线![]() 对
对
称. 设直线![]() 的斜率为
的斜率为![]() , 则直线
, 则直线![]() 的斜率为
的斜率为![]() .
.
所以直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
设点![]() ,
, ![]() ,
,
由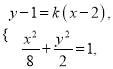 消去
消去![]() ,得
,得![]() . ①
. ①
因为点![]() 在椭圆
在椭圆![]() 上, 所以
上, 所以![]() 是方程①的一个根, 则
是方程①的一个根, 则![]() ,
,
所以![]() .
.
同理![]() .
.
所以![]() .
.
又![]() .
.
所以直线![]() 的斜率为
的斜率为![]() .
.
所以直线![]() 的斜率为定值,该值为
的斜率为定值,该值为![]() .
.
法2:设点![]() ,
,
则直线![]() 的斜率
的斜率![]() , 直线
, 直线![]() 的斜率
的斜率![]() .
.
因为![]() 的角平分线总垂直于
的角平分线总垂直于![]() 轴, 所以
轴, 所以![]() 与
与![]() 所在直线关于直线
所在直线关于直线![]() 对称.
对称.
所以![]() , 即
, 即![]() , ①
, ①
因为点![]() 在椭圆
在椭圆![]() 上,
上,
所以![]() ,②
,②
![]() . ③
. ③
由②得![]() , 得
, 得![]() , ④
, ④
同理由③得![]() , ⑤
, ⑤
由①④⑤得![]() ,
,
化简得![]() , ⑥
, ⑥
由①得![]() , ⑦
, ⑦
⑥![]() ⑦得
⑦得![]() .
.
②![]()
![]() ,得
,得![]() .
.
所以直线![]() 的斜率为
的斜率为![]() 为定值.
为定值.
法3:设直线![]() 的方程为
的方程为![]() ,点
,点![]() ,
,
则![]() ,
,
直线![]() 的斜率
的斜率![]() , 直线
, 直线![]() 的斜率
的斜率![]() .
.
因为![]() 的角平分线总垂直于
的角平分线总垂直于![]() 轴, 所以
轴, 所以![]() 与
与![]() 所在直线关于直线
所在直线关于直线![]() 对称.
对称.
所以![]() , 即
, 即![]() ,
,
化简得![]() .
.
把![]() 代入上式, 并化简得
代入上式, 并化简得
![]() . (*)
. (*)
由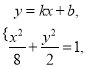 消去
消去![]() 得
得![]() , (**)
, (**)
则![]() ,
,
代入(*)得![]() ,
,
整理得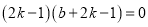 ,
,
所以![]() 或
或![]() .
.
若![]() , 可得方程(**)的一个根为
, 可得方程(**)的一个根为![]() ,不合题意.
,不合题意.
若![]() 时, 合题意.
时, 合题意.
所以直线![]() 的斜率为定值,该值为
的斜率为定值,该值为![]() .
.


 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为集合A,B={x|x<a}.
的定义域为集合A,B={x|x<a}.
(1)求集合A;
(2)若AB,求a的取值范围;
(3)若全集U={x|x≤4},a=-1,求U A及A∩(U B).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 经过点
经过点![]() ,离心率
,离心率![]() ,直线
,直线![]() 的方程为
的方程为 ![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)经过椭圆右焦点![]() 的任一直线(不经过点
的任一直线(不经过点![]() )与椭圆交于两点
)与椭圆交于两点![]() ,
,![]() ,设直线
,设直线![]() 与
与![]() 相交于点
相交于点![]() ,记
,记![]() 的斜率分别为
的斜率分别为![]() ,问:
,问:![]() 是否为定值,若是,求出此定值,若不是,请说明理由.
是否为定值,若是,求出此定值,若不是,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三个内角A、B、C所对的边分别是a、b、c,向量m=(cos B,cos C),n=(2a+c,b),且m⊥n.
(1)求角B的大小;
(2)若b=![]() ,求a+c的取值范围.
,求a+c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4;坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点, ![]() 轴正半轴为极轴的极坐标中,曲线
轴正半轴为极轴的极坐标中,曲线![]() .
.
(Ⅰ)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程.
的直角坐标方程.
(Ⅱ)求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产的某种产品被检测出其中一项质量指标存在问题.该企业为了检查生产该产品的甲,乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.表1是甲流水线样本的频数分布表,图1是乙流水线样本的频率分布直方图.
内,则为合格品,否则为不合格品.表1是甲流水线样本的频数分布表,图1是乙流水线样本的频率分布直方图.
(Ⅰ)根据图1,估计乙流水线生产产品该质量指标值的中位数;
(Ⅱ)若将频率视为概率,某个月内甲,乙两条流水线均生产了5000件产品,则甲,乙两条流水线分别生产出不合格品约多少件?
(Ⅲ)根据已知条件完成下面![]() 列联表,并回答是否有85%的把握认为“该企业生产的这种产品的质量指标值与甲,乙两条流水线的选择有关”?
列联表,并回答是否有85%的把握认为“该企业生产的这种产品的质量指标值与甲,乙两条流水线的选择有关”?
甲生产线 | 乙生产线 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
附:![]() (其中
(其中![]() 为样本容量)
为样本容量)
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥![]() 的底面为矩形,D为
的底面为矩形,D为![]() 的中点,AC⊥平面BCC1B1.
的中点,AC⊥平面BCC1B1.
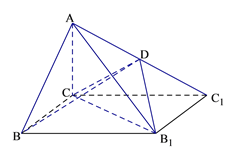
(Ⅰ)证明:AB//平面CDB1;
(Ⅱ)若AC=BC=1,BB1=![]() ,
,
(1)求BD的长;
(2)求B1D与平面ABB1所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知如图,六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABCDEF.则下列结论不正确的是( )
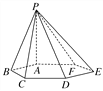
A. CD∥平面PAF
B. DF⊥平面PAF
C. CF∥平面PAB
D. CF⊥平面PAD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com