
三角形的面积为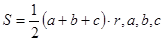 为三角形的边长,r为三角形内切圆的半径,利用类比推理,可得出四面体的体积为( )
为三角形的边长,r为三角形内切圆的半径,利用类比推理,可得出四面体的体积为( )
A.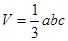
B.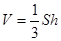
C.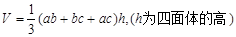
D.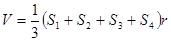 (
(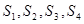 分别为四面体的四个面的面积,r为四面体内切球的半径)
分别为四面体的四个面的面积,r为四面体内切球的半径)
D
【解析】
试题分析:根据平面与空间之间的类比推理,由点类比点或直线,由直线 类比 直线或平面,由内切圆类比内切球,由平面图形面积类比立体图形的体积,结合求三角形的面积的方法类比求四面体的体积即可.解:设四面体的内切球的球心为O,则球心O到四个面的距离都是r,根据三角形的面积的求解方法:分割法,将O与四顶点连起来,可得四面体的体积等于以O为顶点,分别以四个面为底面的4个三棱锥体积的和,∴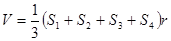 ,故选D.
,故选D.
考点:类比推理
点评:类比推理是指依据两类数学对象的相似性,将已知的一类数学对象的性质类比迁移到另一类数学对象上去.一般步骤:①找出两类事物之间的相似性或者一致性.②用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(或猜想)


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
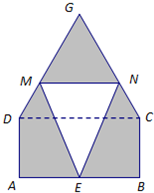 (2013•静安区一模)某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=1米;上部CDG是等边三角形,固定点E为AB的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆.
(2013•静安区一模)某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=1米;上部CDG是等边三角形,固定点E为AB的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆.查看答案和解析>>
科目:高中数学 来源: 题型:
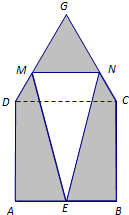 (2013•静安区一模)某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是正方形,其中AB=2米;上部CDG是等边三角形,固定点E为AB的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆.
(2013•静安区一模)某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是正方形,其中AB=2米;上部CDG是等边三角形,固定点E为AB的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆.查看答案和解析>>
科目:高中数学 来源:2002年全国各省市高考模拟试题汇编 题型:044
设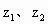 ∈C,且
∈C,且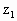 满足
满足![]() ,
,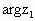 ∈(
∈( ,π).
,π).
(Ⅰ)求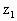 的三角形式;
的三角形式;
(Ⅱ)设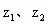 分别对应复平面上点
分别对应复平面上点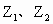 ,且
,且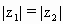 ,arg(
,arg(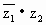 )=
)=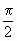 ,求
,求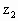 及三角形
及三角形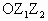 的面积(O为坐标原点).
的面积(O为坐标原点).
查看答案和解析>>
科目:高中数学 来源:2013年上海市静安区高考数学一模试卷(理科)(解析版) 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2013年上海市静安区高考数学一模试卷(文科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com