
【题目】若函数![]() 是定义在实数集
是定义在实数集![]() 上的奇函数,并且在区间
上的奇函数,并且在区间![]() 上是单调递增的函数.
上是单调递增的函数.
(1)研究并证明函数![]() 在区间
在区间![]() 上的单调性;
上的单调性;
(2)若实数![]() 满足不等式
满足不等式![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)设![]() ,则
,则![]() ,所以
,所以![]() ,根据
,根据![]() 在区间
在区间![]() 上是单调递增,可得
上是单调递增,可得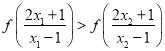 ,从而可得函数
,从而可得函数![]() 在区间
在区间![]() 上是单调递减函数;(2)先证明
上是单调递减函数;(2)先证明![]() 在区间
在区间![]() 上是单调递增的函数,根据奇偶性可得
上是单调递增的函数,根据奇偶性可得![]() 在区间
在区间![]() 上是单调递增的函数,再将
上是单调递增的函数,再将![]() 变形为
变形为![]() ,可得
,可得![]() ,进而可得实数
,进而可得实数![]() 的取值范围.
的取值范围.
试题解析:(1)设![]() ,
, ![]() 显然
显然![]() 恒成立.
恒成立.
设![]() ,则
,则![]() ,
, ![]() ,
, ![]() ,
,
则![]() ,
,
所以![]() ,
,
又![]() 在区间
在区间![]() 上是单调递增,所以
上是单调递增,所以![]() ,
,
即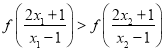 ,
,
所以函数![]() 在区间
在区间![]() 上是单调递减函数.
上是单调递减函数.
(2)因为![]() 是定义在实数集
是定义在实数集![]() 上的奇函数,所以
上的奇函数,所以![]() ,
,
又因为![]() 在区间
在区间![]() 上是单调递增的函数,
上是单调递增的函数,
所以当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() ,
,
所以当![]() ,有
,有![]() .
.
设![]() ,则
,则![]() ,所以
,所以![]() ,
,
即![]() ,所以
,所以![]() ,
,
所以![]() 在区间
在区间![]() 上是单调递增的函数.
上是单调递增的函数.
综上所述, ![]() 在区间
在区间![]() 上是单调递增的函数.
上是单调递增的函数.
所以由![]() 得
得![]() ,
,
即![]() 所以
所以![]() .
.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案科目:高中数学 来源: 题型:
【题目】定义:若函数![]() 的定义域为
的定义域为![]() ,且存在非零常数
,且存在非零常数![]() ,对任意
,对任意![]() ,
, ![]() 恒成立,则称
恒成立,则称![]() 为线周期函数,
为线周期函数, ![]() 为
为![]() 的线周期.
的线周期.
(Ⅰ)下列函数①![]() ,②
,②![]() ,③
,③![]() (其中
(其中![]() 表示不超过
表示不超过![]() 的最大整数),是线周期函数的是(直接填写序号);
的最大整数),是线周期函数的是(直接填写序号);
(Ⅱ)若![]() 为线周期函数,其线周期为
为线周期函数,其线周期为![]() ,求证:函数
,求证:函数![]() 为周期函数;
为周期函数;
(Ⅲ)若![]() 为线周期函数,求
为线周期函数,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆C的两个焦点是F1、F2 , 过F1的直线与椭圆C交于P、Q,若|PF2|=|F1F2|,且5|PF1|=6|F1Q|,则椭圆的离心率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于空间两不同的直线![]() ,两不同的平面
,两不同的平面![]() ,有下列推理:
,有下列推理:
(1)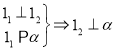 , (2)
, (2)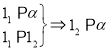 ,(3)
,(3)![]()
(4)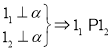 , (5)
, (5)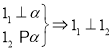
其中推理正确的序号为( )
A. (1)(3)(4) B. (2)(3)(5) C. (4)(5) D. (2)(3)(4)(5)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接2017年“双11”,“双12”购物狂欢节的来临,某青花瓷生产厂家计划每天生产汤碗、花瓶、茶杯这三种瓷器共100个,生产一个汤碗需5分钟,生产一个花瓶需7分钟,生产一个茶杯需4分钟,已知总生产时间不超过10小时.若生产一个汤碗可获利润5元,生产一个花瓶可获利润6元,生产一个茶杯可获利润3元.
(1)使用每天生产的汤碗个数x与花瓶个数y表示每天的利润ω(元);
(2)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且![]()
(1)求证:不论![]() 为何值,总有平面BEF⊥平面ABC;
为何值,总有平面BEF⊥平面ABC;
(2)当λ为何值时,平面BEF⊥平面ACD ?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,圆
,圆![]() .
.
(Ⅰ)若直线![]() 过点
过点![]() 且到圆心
且到圆心![]() 的距离为1,求直线
的距离为1,求直线![]() 的方程;
的方程;
(Ⅱ)设过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于
交于![]() 两点(
两点(![]() 的斜率为正),当
的斜率为正),当![]() 时,求以线段
时,求以线段![]() 为直径的圆的方程.
为直径的圆的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com