
(本题满分12分)
某市统计局就某地居民的月收入调查了10000人,他们的月收入均在 内.现根据所得数据画出了该样本的频率分布直方图如下.(每个分组包括左端点,不包括右端点,如第一组表示月收入在
内.现根据所得数据画出了该样本的频率分布直方图如下.(每个分组包括左端点,不包括右端点,如第一组表示月收入在 内)
内)
(1)求某居民月收入在 内的频率;
内的频率;
(2)根据该频率分布直方图估计居民的月收入的中位数;
(3)为了分析居民的月收入与年龄、职业等方面的关系,需再从这10000人中利用分层抽样的方法抽取100人作进一步分析,则应从月收入在 内的居民中抽取多少人?
内的居民中抽取多少人?
(1) 0.25 (2) 2500(3)15
解析试题分析:(1) 由频率分布直方图可知,居民月收入在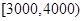 内的频率为(0.0002+0.0003)×500=0.25. ……………………2分
内的频率为(0.0002+0.0003)×500=0.25. ……………………2分
(2) 由频率分布直方图可知
0.0001×500=0.05,
0.0004×500=0.20,
0.0005×500=0.25,
从而有0.0001×500+0.0004×500+0.0005×500="0.5," ……………………6分
所以可以估计居民的月收入的中位数为2500(元). ………………7分
(3) 由频率分布直方图可知,居民月收入在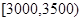 内的频率为
内的频率为
0.0003×500=0.15, ……………………9分
所以这10000人中月收入在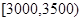 内的人数为0.15×10000=1500(人),
内的人数为0.15×10000=1500(人),
……………………11分
再从这10000人中利用分层抽样的方法抽取100人,则应从月收入在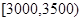 内的居民中抽取
内的居民中抽取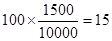 (人). ……………………12分
(人). ……………………12分
考点:由频率分布直方图求各组频率中位数
点评:频率分布直方图中每一个小矩形的面积等于该组的频率,所有小矩形面积之和为1,中位数即面积为0.5处对应的横坐标


科目:高中数学 来源: 题型:解答题
某校的研究性学习小组为了研究高中学生的身体发育状况,在该校随机抽出120名17至18周岁的男生,其中偏重的有60人,不偏重的也有60人。在偏重的60人中偏高的有40人,不偏高的有20人;在不偏重的60人中偏高和不偏高人数各占一半
(1)根据以上数据建立一个 列联表:
| | 偏重 | 不偏重 | 合计 |
| 偏高 | | | |
| 不偏高 | | | |
| 合计 | | | |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人。女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动。
(1)根据以上数据建立一个2×2的列联表;
(2)判断性别与休闲方式是否有关系。
附:
 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某大学体育学院在2012年新招的大一学生中,随机抽取了 40名男生,他们的身高(单位:cm)情况共分成五组:第1组[175,180),第 2 组[180,185),第 3 组 [185,190),第 4 组[190,195),第 5 组[195,200) .得到的频率分布直方图(局部)如图所示,同时规定身高在185cm以上(含185cm)的学生成为组建该校篮球队的“预备生”.
(I)求第四组的频率并补布直方图;
(II)如果用分层抽样的方法从“预备生”和“非预备生”中选出5人,再从这5人中随机选2人,那么至少有1人是“预备生”的概率是多少?
(III)若该校决定在第4,5组中随机抽取2名学生接受技能测试,第5组中有ζ名学生接受测试,试求ζ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题共12分)
现对某市工薪阶层关于“楼市限购令”的态度进行调查,随机抽调了50人,他们月收入的频数分布及对“楼市限购令”赞成人数如下表.
| 月收入(单位百元) | [15,25 | [25,35 | [35,45 | [45,55 | [55,65 | [65,75 |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 8 | 12 | 5 | 2 | 1 |
| | 月收入不低于55百元的人数 | 月收入低于55百元的人数 | 合计 |
| 赞成 |  |  | |
| 不赞成 |  |  | |
| 合计 | | | |
 ,求随机变量
,求随机变量 的分布列。
的分布列。

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国
是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国 标准采用世卫组织设定的最宽限值,
标准采用世卫组织设定的最宽限值, 日均值在35微克/立方米以下空气质量为一级;在35微克/立方米
日均值在35微克/立方米以下空气质量为一级;在35微克/立方米 75微克/立方米之间空气质量为二级;在75微克/立方米及其以上空气质量为超标.
75微克/立方米之间空气质量为二级;在75微克/立方米及其以上空气质量为超标.
某试点城市环保局从该市市区2011年全年每天的 监测数据中随机抽取6天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶),若从这6天的数据中随机抽出2天.
监测数据中随机抽取6天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶),若从这6天的数据中随机抽出2天.
(Ⅰ)求恰有一天空气质量超标的概率;
(Ⅱ)求至多有一天空气质量超标的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某市的教育研究机构对全市高三学生进行综合素质 测试,随机抽取了部分学生的成绩,得到如图所示的成绩 频率分布直方图.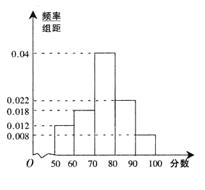
(I )估计全市学生综合素质成绩的平均值;
(II)若评定成绩不低于8o分为优秀.视频率为概率,从 全市学生中任选3名学生(看作有放回的抽样),变量 表示 3名学生中成绩优秀的人数,求变量
表示 3名学生中成绩优秀的人数,求变量 的分布列及期望
的分布列及期望 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是: .
.
(1)求图中x的值;
(2)从成绩不低于80分的学生中随机选取2人,该2人中成绩在90分以上(含90分)的人数记为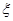 ,求
,求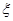 的分布列和数学期望。
的分布列和数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题12分)下表提供了工厂技术改造后某种型号设备的使用年限 和所支出的维修费用
和所支出的维修费用 (万元)的几组对照数据:
(万元)的几组对照数据:
 (年) (年) |  |  |  |  |
 (万元) (万元) |  |  |  |  |
 对
对 呈线性相关关系,请根据上表提供的数据,用最小二乘法求出
呈线性相关关系,请根据上表提供的数据,用最小二乘法求出 关于
关于 的线性回归方程
的线性回归方程 ;
;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com