
【题目】已知四棱锥P﹣ABCD,底面ABCD为正方形,侧面PAD为直角三角形,且PA=PD,面PAD⊥面ABCD,E、F分别为AB、PD的中点. 
(Ⅰ)求证:EF∥面PBC;
(Ⅱ)求证:AP⊥面PCD.
【答案】证明:(I)法1:取PC中点G,连接FG、BG
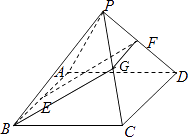
因为F、G分别为PD、PC的中点,
所以FG∥CD且 ![]() ;
;
因为ABCD为正方形,所以BE∥CD,
又因为E为AB中点,所以 ![]() ,
,
所以BE∥FG,且BE=FG,
所以BEFG为平行四边形,所以EF∥BG;
因为EF面PBC,BG面PBC,
所以EF∥面PBC
法2:取CD中点H,连接FH,EH,
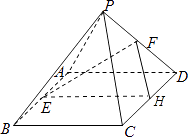
因为F,H分别为PD、CD的中点,
所以FH∥PC,EH∥BC;
又FH平面EFH,EH平面EFH,PC面PBC,BC面PBC,
且FH∩EH=H,
所以平面EFH∥平面PBC,
又因为EF平面EFH,
所以EF∥面PBC;
(II)因为ABCD为正方形,
所以CD⊥AD,
面PAD⊥面ABCD且AD为交线,
所以CD⊥面PAD,
AP面PAD,所以CD⊥AP,
PAD为直角三角形,且PA=PD,
所以PD⊥AP,
又CD∩PD=D,
所以,AP⊥面PCD;
【解析】(I)法1:取PC中点G,连接FG、BG,可得BE∥CD,又 ![]() ,可得BEFG为平行四边形,即证明EF∥BG,进而判定EF∥面PBC;法2:取CD中点H,连接FH,EH,通过证明平面EFH∥平面PBC,进而判定EF∥面PBC.(II)利用线面垂直的性质可得CD⊥AP,进而证明PD⊥AP,即可证明线面垂直.
,可得BEFG为平行四边形,即证明EF∥BG,进而判定EF∥面PBC;法2:取CD中点H,连接FH,EH,通过证明平面EFH∥平面PBC,进而判定EF∥面PBC.(II)利用线面垂直的性质可得CD⊥AP,进而证明PD⊥AP,即可证明线面垂直.
【考点精析】认真审题,首先需要了解直线与平面平行的判定(平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行),还要掌握直线与平面垂直的判定(一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想)的相关知识才是答题的关键.


科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() ,动直线
,动直线 ![]()
(1)若动直线l与椭圆C相交,求实数m的取值范围;
(2)当动直线l与椭圆C相交时,证明:这些直线被椭圆截得的线段的中点都在直线3x+2y=0上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的所对的边分别为a,b,c,且a2+b2=ab+c2 .
(Ⅰ) 求tan(C﹣ ![]() )的值;
)的值;
(Ⅱ) 若c= ![]() ,求S△ABC的最大值.
,求S△ABC的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列选项中,表示同一集合的是( )
A.A={0,1},B={(0,1)}
B.A={2,3},B={3,2}
C.A={x|﹣1<x≤1,x∈N},B={1}
D.![]()
E.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在几何体ABCDE中,BE⊥平面ABC,CD∥BE,△ABC是等腰直角三角形,∠ABC=90°,且BE=AB=4,CD=2,点F在线段AC上,且AF=3FC 
(1)求异面直线DF与AE所成角;
(2)求平面ABC与平面ADE所成二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】光线l1从点M(﹣1,3)射到x轴上,在点P(1,0)处被x轴反射,得到光线l2 , 再经直线x+y﹣4=0反射,得到光线l3 , 求l2和l3的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)的图象如图所示,曲线BCD为抛物线的一部分. 
(Ⅰ)求f(x)解析式;
(Ⅱ)若f(x)=1,求x的值;
(Ⅲ)若f(x)>f(2﹣x),求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且a1=2,an+1= ![]() Sn(n=1,2,3,…).
Sn(n=1,2,3,…).
(1)证明:数列{ ![]() }是等比数列;
}是等比数列;
(2)设bn= ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com