
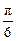 ,且4an-1+an+1=4an,则sina1+sina2+sina3+…+sina2014=
,且4an-1+an+1=4an,则sina1+sina2+sina3+…+sina2014=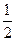 +
+
 q=2
q=2 an=
an= ·2n-1
·2n-1 , a2=
, a2= ·2=
·2= , a3=
, a3=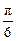 ·22=
·22= ,a4=
,a4=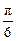 ·23=
·23= ,a5=
,a5= ·24=
·24= , a6=
, a6= ·24=
·24= ,…
,… =
=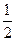 ,sina2=sin
,sina2=sin =
= ,
, = sin(
= sin( )=
)= ,
, ·22)=sin
·22)=sin =sin(
=sin( )=-sin
)=-sin =-
=-
 ·23)=sin
·23)=sin =sin(
=sin( )=sin
)=sin = sin(
= sin( )=
)=
 ·24)=sin
·24)=sin = sin(
= sin( )=sin(
)=sin( )=-sin
)=-sin =-
=-
 ·2n-1=
·2n-1= ·22k-2=
·22k-2= ·4k-1=
·4k-1= ·(1+3)k-1=
·(1+3)k-1= ·(1+
·(1+ 3+
3+ 32+…+
32+…+ 3k-1)
3k-1) +
+ (
( +
+ 31+…+
31+…+ 3k-2)(规定
3k-2)(规定 =0)
=0) +
+ (
( +
+ 31+…+
31+…+ 3k-2)]=sin
3k-2)]=sin = sin(
= sin( )=
)= ,
, ·2n-1=
·2n-1= ·22k-2=
·22k-2= ·4k-1=
·4k-1= ·(1+3)k-1=
·(1+3)k-1= ·(1+
·(1+ 3+
3+ 32+…+
32+…+ 3k-1)
3k-1) +
+ (
( +
+ 31+…+
31+…+ 3k-2)
3k-2) +
+ (
( +
+ 31+…+
31+…+ 3k-2)]= sin
3k-2)]= sin =sin(
=sin( )=-sin
)=-sin =-
=-
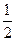 +
+


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com