设
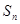
是等差数列
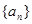
的前n项和,已知
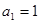
,公差d=2,则
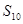
="_______" .
解:因为设
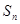
是等差数列
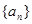
的前n项和,已知
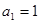
,公差d=2,则
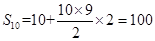
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
若数列
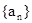
前n项的和
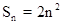
,数列
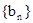
为等比数列,
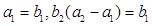
.
(Ⅰ)求数列
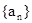
和
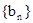
的通项公式;
(Ⅱ)若
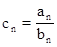
,求
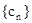
的前n项和
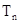
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知{
an}为等差数列,
a1+
a3+
a5=105,
a2+
a4+
a6=99,以
Sn表示数列{
an}的前
n项和,则使得
Sn达到最大值的
n是( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
已知等差数列
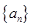
和
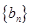
的前n项和分别为

,且

,则使得
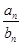
为整数的正整数n的个数是___
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分12分)
已知数列
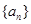
是一个等差数列,且
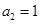
,
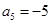
.(1)求
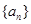
的通项
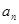
;
(2) 求
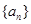
前
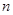
项和
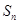
;
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
在等差数列
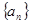
中,设
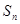
为前
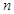
项和,且
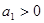
,
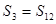
,当
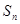
最大时,
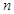
的值为 ( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
设数列
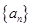
的前
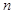
项和为
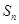
,则下列说法错误的是
.
①若
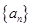
是等差数列,则
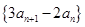
是等差数列;
②若
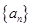
是等差数列,则
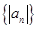
是等差数列;
③若
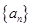
是公比为
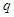
的等比数列,则
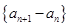
也是等比数列且公比为
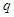
;
④若
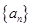
是公比为
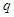
的等比数列,则
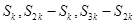
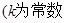
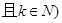
也是等比数列且公比为
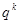
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
.随机变量
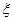
的分布列为,
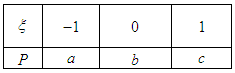
其中
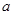
、
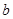
、
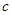
成等差数列,若
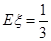
,则
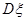
=
查看答案和解析>>

 阅读快车系列答案
阅读快车系列答案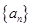 的前
的前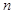 项和为
项和为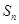 ,则下列说法错误的是 .
,则下列说法错误的是 .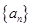 是等差数列,则
是等差数列,则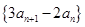 是等差数列;
是等差数列;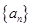 是等差数列,则
是等差数列,则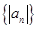 是等差数列;
是等差数列;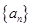 是公比为
是公比为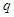 的等比数列,则
的等比数列,则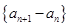 也是等比数列且公比为
也是等比数列且公比为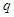 ;
;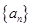 是公比为
是公比为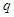 的等比数列,则
的等比数列,则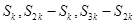
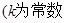
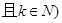 也是等比数列且公比为
也是等比数列且公比为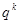 .
.