
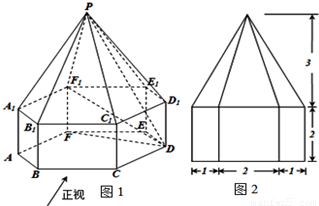
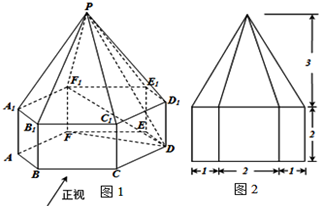
 (1)解:由题意可知,该几何体由下部正六棱柱和上部正六棱锥组合而成,
(1)解:由题意可知,该几何体由下部正六棱柱和上部正六棱锥组合而成,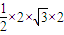 =
=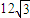 ; …(3分)
; …(3分)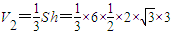 =
=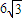 ; …(6分)
; …(6分) . …(7分)
. …(7分)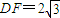 ,∴DF1=4,
,∴DF1=4,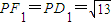 ;
;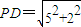 =
=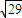 ,
,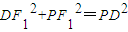 ,故DF1⊥PF1;…(13分)
,故DF1⊥PF1;…(13分)

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
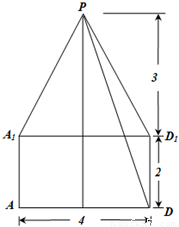
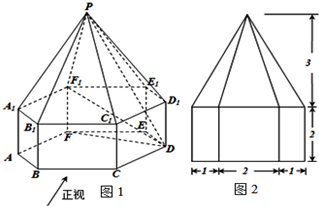 (2011•佛山二模)如图1,已知几何体的下部是一个底面为正六边形、侧面全为矩形的棱柱,上部是一个侧面全为等腰三角形的棱锥,图2是该几何体的主视图.
(2011•佛山二模)如图1,已知几何体的下部是一个底面为正六边形、侧面全为矩形的棱柱,上部是一个侧面全为等腰三角形的棱锥,图2是该几何体的主视图.查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省高考猜押题卷文科数学(一)解析版 题型:选择题
如图1,已知E、F、G、H分别是正方体 的棱
的棱 、
、 、
、 、
、 的中点,平面EFGH将正方体截去一个三棱柱后,得到图2所示的几何体,则此几何体的正视图和侧视图是( )
的中点,平面EFGH将正方体截去一个三棱柱后,得到图2所示的几何体,则此几何体的正视图和侧视图是( )

查看答案和解析>>
科目:高中数学 来源:佛山二模 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com