
【题目】已知 ![]() 、
、 ![]() 是两个不共线的向量,且
是两个不共线的向量,且 ![]() =(cosα,sinα),
=(cosα,sinα), ![]() =(cosβ,sinβ).
=(cosβ,sinβ).
(1)求证: ![]() +
+ ![]() 与
与 ![]() ﹣
﹣ ![]() 垂直;
垂直;
(2)若α∈(﹣ ![]() ,
, ![]() ),β=
),β= ![]() ,且|
,且| ![]() +
+ ![]() |=
|= ![]() ,求sinα.
,求sinα.
【答案】
(1)证明: ![]() 、
、 ![]() 是两个不共线的向量,
是两个不共线的向量,
且 ![]() =(cosα,sinα),
=(cosα,sinα), ![]() =(cosβ,sinβ),.
=(cosβ,sinβ),.
∴ ![]() +
+ ![]() =(cosα+cosβ,sinα+sinβ),
=(cosα+cosβ,sinα+sinβ),
![]() ﹣
﹣ ![]() =(cosα﹣cosβ,sinα﹣sinβ),
=(cosα﹣cosβ,sinα﹣sinβ),
∴( ![]() +
+ ![]() )(
)( ![]() ﹣
﹣ ![]() )=(cos2﹣cos2β)+(sin2α﹣sin2β)
)=(cos2﹣cos2β)+(sin2α﹣sin2β)
=(cos2α+sin2α)﹣(cos2β+sin2β)
=1﹣1=0,
∴ ![]() +
+ ![]() 与
与 ![]() ﹣
﹣ ![]() 垂直
垂直
(2)解:∵ ![]() =(cosα+cosβ)2+(sinα+sinβ)2
=(cosα+cosβ)2+(sinα+sinβ)2
=2+2(cosαcosβ+sinαsinβ)
=2+2cos(α﹣β),
且β= ![]() ,|
,| ![]() +
+ ![]() |=
|= ![]() ,
,
∴2+2cos(α﹣ ![]() )=
)= ![]() ,
,
解得cos(α﹣ ![]() )=
)= ![]() ;
;
又α∈(﹣ ![]() ,
, ![]() ),
),
∴α﹣ ![]() ∈(﹣
∈(﹣ ![]() ,0),
,0),
∴sin(α﹣ ![]() )=﹣
)=﹣ 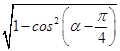 =﹣
=﹣ ![]() ,
,
∴sinα=sin[(α﹣ ![]() )+
)+ ![]() ]=sin(α﹣
]=sin(α﹣ ![]() )cos
)cos ![]() +cos(α﹣
+cos(α﹣ ![]() )sin
)sin ![]()
=﹣ ![]() ×
× ![]() +
+ ![]() ×
× ![]() =﹣
=﹣ ![]()
【解析】(1)利用平面向量的坐标运算与数量积为0,即可证明 ![]() +
+ ![]() 与
与 ![]() ﹣
﹣ ![]() 垂直;(2)利用平面向量的数量积与模长公式,结合三角恒等变换与同角的三角函数关系,即可求出sinα的值.
垂直;(2)利用平面向量的数量积与模长公式,结合三角恒等变换与同角的三角函数关系,即可求出sinα的值.


科目:高中数学 来源: 题型:
【题目】圆C满足:①圆心C在射线y=2x(x>0)上; ②与x轴相切;
③被直线y=x+2截得的线段长为 ![]()
(1)求圆C的方程;
(2)过直线x+y+3=0上一点P作圆C的切线,设切点为E、F,求四边形PECF面积的最小值,并求此时 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:方程x2﹣2x+m=0有两个不相等的实数根;命题q:函数y=(m+2)x﹣1是R上的单调增函数.若“p或q”是真命题,“p且q”是假命题,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() ,动直线
,动直线 ![]()
(1)若动直线l与椭圆C相交,求实数m的取值范围;
(2)当动直线l与椭圆C相交时,证明:这些直线被椭圆截得的线段的中点都在直线3x+2y=0上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1的方程为3x+4y﹣12=0.
(1)若直线l2与l1平行,且过点(﹣1,3),求直线l2的方程;
(2)若直线l2与l1垂直,且l2与两坐标轴围成的三角形面积为4,求直线l2的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的所对的边分别为a,b,c,且a2+b2=ab+c2 .
(Ⅰ) 求tan(C﹣ ![]() )的值;
)的值;
(Ⅱ) 若c= ![]() ,求S△ABC的最大值.
,求S△ABC的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)的图象如图所示,曲线BCD为抛物线的一部分. 
(Ⅰ)求f(x)解析式;
(Ⅱ)若f(x)=1,求x的值;
(Ⅲ)若f(x)>f(2﹣x),求x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com