
【题目】已知直线l经过点![]() .
.
(1)若直线![]() 在两坐标轴上的截距相等,求直线
在两坐标轴上的截距相等,求直线![]() 的方程;
的方程;
(2)若![]() ,
,![]() 两点到直线
两点到直线![]() 的距离相等,求直线
的距离相等,求直线![]() 的方程.
的方程.
【答案】(1)![]() 或
或![]() (2)
(2)![]() 或
或![]()
【解析】
(1)讨论直线是否过原点,利用截距相等进行求解即可.
(2)根据点到直线的距离相等,分直线平行和直线过A,B的中点两种情况进行求解即可.
(1)若直线过原点,则设为y=kx,则k=2,此时直线方程为y=2x,
当直线不过原点,设方程为![]() 1,即x+y=a,
1,即x+y=a,
此时a=1+2=3,则方程为x+y=3,
综上直线方程为y=2x或x+y=3.
(2)若A,B两点在直线l同侧,
则AB∥l,
AB的斜率k![]() 1,
1,
即l的斜率为1,
则l的方程为y﹣2=x﹣1,即y=x+1,
若A,B两点在直线的两侧,即l过A,B的中点C(2,0),
则k![]() 2,
2,
则l的方程为y﹣0=﹣2(x﹣2),即y=﹣2x+4,
综上l的方程为y=﹣2x+4或y=x+1.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】(选修4﹣4:坐标系与参数方程)
在直角坐标系xOy中,椭圆C的参数方程为 ![]() 为参数,a>b>0).在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,直线l与圆O的极坐标方程分别为
为参数,a>b>0).在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,直线l与圆O的极坐标方程分别为 ![]() 为非零常数)与ρ=b.若直线l经过椭圆C的焦点,且与圆O相切,则椭圆C的离心率为 .
为非零常数)与ρ=b.若直线l经过椭圆C的焦点,且与圆O相切,则椭圆C的离心率为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电影院共有![]() 个座位.某天,这家电影院上、下午各演一场电影.看电影的是甲、乙、丙三所中学的学生,三所学校的观影人数分别是985人, 1010人,2019人(同一所学校的学生有的看上午场,也有的看下午场,但每人只能看一-场).已知无论如何排座位,这天观影时总存在这样的一个座位,上、 下午在这个座位上坐的是同一所学校的学生,那么
个座位.某天,这家电影院上、下午各演一场电影.看电影的是甲、乙、丙三所中学的学生,三所学校的观影人数分别是985人, 1010人,2019人(同一所学校的学生有的看上午场,也有的看下午场,但每人只能看一-场).已知无论如何排座位,这天观影时总存在这样的一个座位,上、 下午在这个座位上坐的是同一所学校的学生,那么![]() 的可能取值有( )
的可能取值有( )
A. 12个 B. 11个 C. 10个 D. 前三个答案都不对
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当x∈R,|x|<1时,有如下表达式:1+x+x2+…+xn+…= ![]()
两边同时积分得: ![]() dx+
dx+ ![]() xdx+
xdx+ ![]() x2dx+…+
x2dx+…+ ![]() xndx+…=
xndx+…= ![]()
![]() dx
dx
从而得到如下等式:1× ![]() +
+ ![]() ×(
×( ![]() )2+
)2+ ![]() ×(
×( ![]() )3+…+
)3+…+ ![]() ×(
×( ![]() )n+1+…=ln2
)n+1+…=ln2
请根据以上材料所蕴含的数学思想方法,计算:![]() ×
× ![]() +
+ ![]()
![]() ×(
×( ![]() )2+
)2+ ![]()
![]() ×(
×( ![]() )3+…+
)3+…+ ![]()
![]() ×(
×( ![]() )n+1= .
)n+1= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测试中,卷面满分为100分,考生得分为整数,规定60分及以上为及格.某调研课题小组为了调查午休对考生复习效果的影响,对午休和不午休的考生进行了测试成绩的统计,数据如下表:

(1)根据上述表格完成下列列联表:

(2)判断“能否在犯错误的概率不超过0.010的前提下认为成绩及格与午休有关”?
(参考公式:![]() ,其中
,其中![]() .)
.)
| 0.010 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司针对企业职工推出一款意外险产品,每年每人只要交少量保费,发生意外后可一次性获赔50万元.保险公司把职工从事的所有岗位共分为![]() 、
、![]() 、
、![]() 三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).
三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).


(Ⅰ)根据规定,该产品各工种保单的期望利润都不得超过保费的20%,试分别确定各类工种每张保单保费的上限;
(Ⅱ)某企业共有职工20000人,从事三类工种的人数分布比例如图,老板准备为全体职工每人购买一份此种保险,并以(Ⅰ)中计算的各类保险上限购买,试估计保险公司在这宗交易中的期望利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高三年级学生某次身体素质体能测试的原始成绩采用百分制,已知所有这些学生的原始成绩均分布在![]() 内,发布成绩使用等级制,各等级划分标准见下表.
内,发布成绩使用等级制,各等级划分标准见下表.
百分制 | 85分及以上 | 70分到84分 | 60分到69分 | 60分以下 |
等级 | A | B | C | D |
规定:A,B,C三级为合格等级,D为不合格等级为了解该校高三年级学生身体素质情况,从中抽取了n名学生的原始成绩作为样本进行统计.
按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示
的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示
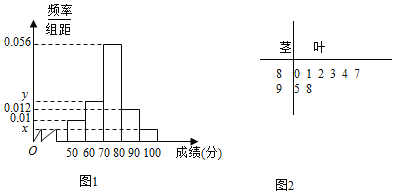
![]() 求n和频率分布直方图中的x,y的值,并估计该校高一年级学生成绩是合格等级的概率;
求n和频率分布直方图中的x,y的值,并估计该校高一年级学生成绩是合格等级的概率;
![]() 根据频率分布直方图,求成绩的中位数
根据频率分布直方图,求成绩的中位数![]() 精确到
精确到![]() ;
;
![]() 在选取的样本中,从A,D两个等级的学生中随机抽取2名学生进行调研,求至少有一名学生是A等级的概率.
在选取的样本中,从A,D两个等级的学生中随机抽取2名学生进行调研,求至少有一名学生是A等级的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com