
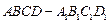 的上底面上叠放三棱柱
的上底面上叠放三棱柱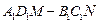 ,该几何体的正视图与左视图如右图所示.
,该几何体的正视图与左视图如右图所示.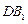
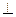
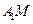 ,求实数
,求实数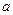 的值;
的值;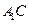
 平面
平面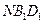 ;
;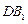 与平面
与平面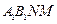 所成角的正弦值
所成角的正弦值
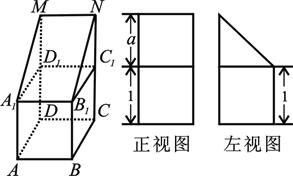
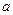 =1
=1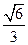 .
.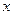 、y、z轴,建立空间直角坐标系,则D(0,0,0),B1
、y、z轴,建立空间直角坐标系,则D(0,0,0),B1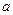 ),
),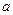 ).
).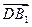 =(1,1,1),
=(1,1,1),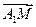 =(-1,0,
=(-1,0,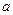 ).
).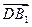 ⊥
⊥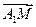 ,
,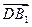 ·
·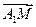 ="0 "
="0 " 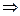 -1+a="0 "
-1+a="0 " 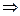
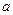 ="1." ---------------------4分
="1." ---------------------4分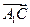 =(-1,1,-1),
=(-1,1,-1),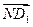 =(0,
=(0,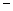 1,
1,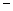 1),
1),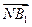 =(1,0,
=(1,0,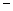 1).
1).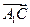 ·
·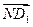 =0,
=0, 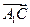 ·
·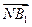 =0,
=0,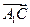 ⊥
⊥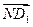 ,
, 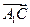 ⊥
⊥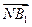 ,又ND1
,又ND1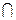 NB1=N.
NB1=N.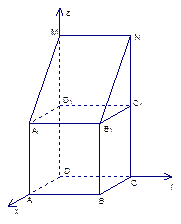 ②设平面A1B1NM的法向量为
②设平面A1B1NM的法向量为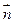 =(x、y、z),
=(x、y、z),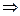
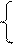
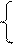
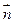 ·
·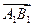 ="0" y=0
="0" y=0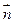 ·
·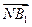 ="0 " x-z="0" .
="0 " x-z="0" . 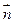 =(1,0,1),又
=(1,0,1),又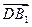 =(1,1,1),
=(1,1,1),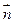 ·
·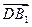 >=
>=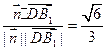 .
.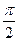 -<
-<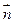 ·
·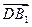 >)
>)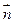 ·
·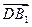 >=
>=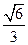 .----------------------------13分
.----------------------------13分

科目:高中数学 来源:不详 题型:解答题
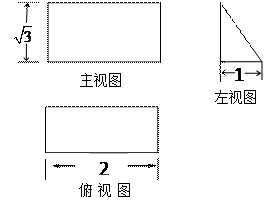
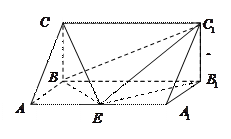
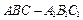 直观图和三视图如图所示(主视图、俯视图都是矩形,左视图是直角三角形),设
直观图和三视图如图所示(主视图、俯视图都是矩形,左视图是直角三角形),设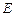 、
、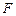 分别为
分别为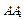 和
和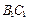 的中点.
的中点.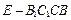 的体积;
的体积;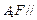 平面
平面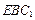 ;
;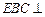 平面
平面 .
.
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 的纬线上,且两地的经度差为
的纬线上,且两地的经度差为 ,若地球的半径为
,若地球的半径为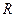 千米,且时速为20千米的轮船从A地到B地最少需要
千米,且时速为20千米的轮船从A地到B地最少需要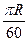 小时,则
小时,则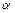 为
为 A.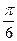 | B.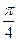 | C.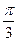 | D.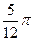 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
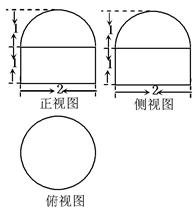
A.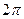 | B.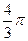 | C.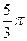 | D.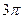 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com