
【题目】已知函数f(x)=(x2+ax+b)ex , 当b<1时,函数f(x)在(﹣∞,﹣2),(1,+∞)上均为增函数,则 ![]() 的取值范围是 .
的取值范围是 .
【答案】(﹣3,﹣ ![]() ]
]
【解析】解:由f′(x)=[x2+(a+2)x+a+b]ex
函数f(x)在(﹣∞,﹣2),(1,+∞)增函数,
∴x2+(a+2)x+a+b>0恒成立,
∴ ![]() ,
,
∴ ![]() ,
,
画出满足条件的平面区域,如图所示:
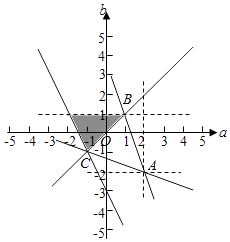 ,
,
由 ![]() ,解得B(1,1),
,解得B(1,1),
由 ![]() ,解得C(﹣1,﹣1),
,解得C(﹣1,﹣1),
结合图象 ![]() 的几何意义表示过A(2,﹣2)与平面区域内的点的直线的斜率,
的几何意义表示过A(2,﹣2)与平面区域内的点的直线的斜率,
而KAB=﹣3,KAC=﹣ ![]() ,
,
故 ![]() 的取值范围是(﹣3,﹣
的取值范围是(﹣3,﹣ ![]() ],
],
所以答案是:(﹣3,﹣ ![]() ].
].
【考点精析】关于本题考查的利用导数研究函数的单调性,需要了解一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能得出正确答案.
在这个区间单调递减才能得出正确答案.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)求证: ![]() ;
;
(3)判断曲线y=f(x)是否位于x轴下方,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 若存在互不相同的四个实数0<a<b<c<d满足f(a)=f(b)=f(c)=f(d),则ab+c+2d的取值范围是( )
若存在互不相同的四个实数0<a<b<c<d满足f(a)=f(b)=f(c)=f(d),则ab+c+2d的取值范围是( )
A.( ![]() ,
, ![]() )
)
B.( ![]() ,15)
,15)
C.[ ![]() ,15]
,15]
D.( ![]() ,15)
,15)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x2﹣x﹣1)ex .
(1)求函数f(x)的单调区间.
(2)若方程a( ![]() +1)+ex=ex在(0,1)内有解,求实数a的取值范围.
+1)+ex=ex在(0,1)内有解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax(lnx﹣1)(a≠0).
(1)求函数y=f(x)的单调递增区间;
(2)当a>0时,设函数g(x)= ![]() x3﹣f(x),函数h(x)=g′(x),
x3﹣f(x),函数h(x)=g′(x),
①若h(x)≥0恒成立,求实数a的取值范围;
②证明:ln(1×2×3×…×n)2e<12+22+32+…+n2(n∈N*).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知公比为q的等比数列{an}的前6项和S6=21,且4a1 , ![]() ,a2成等差数列.
,a2成等差数列.
(1)求an;
(2)设{bn}是首项为2,公差为﹣a1的等差数列,记{bn}前n项和为Tn , 求Tn的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学在上学路上要经过A、B、C三个带有红绿灯的路口.已知他在A、B、C三个路口遇到红灯的概率依次是 ![]() 、
、 ![]() 、
、 ![]() ,遇到红灯时停留的时间依次是40秒、20秒、80秒,且在各路口是否遇到红灯是相互独立的.
,遇到红灯时停留的时间依次是40秒、20秒、80秒,且在各路口是否遇到红灯是相互独立的.
(1)求这名同学在上学路上在第三个路口首次遇到红灯的概率;,
(2)求这名同学在上学路上因遇到红灯停留的总时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com