
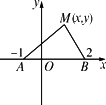
如图所示,点A(-1,0),B(2,0),动点M满足2∠MAB=∠MBA,求点M的轨迹方程.
|
解析:设点M(x,y),∠MAB=α,则 ∠MBA=2α,tanα=kMA= tan(π-2α)=kMB= ∴-tan2α= 将tanα= 化简得y=0或 (1)因为∠MBA=2∠MAB, ∴|MA|>|MB|,则x≥1,∴ (2)当∠MBA=90°时,MB斜率不存在,此时△MAB为等腰Rt△,点M(2,3)或 (3)当点M为线段AB内分点时,满足题设∠MBA=2∠MAB, ∴y=0且-1<x<2. (4)点M在x轴下方时,∠MBA为MB倾斜角,此时MA倾斜角为π-∠MAB,用同样方法,可求得上述方程. 综上所述,点M轨迹方程为 |


科目:高中数学 来源: 题型:
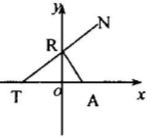 如图所示,点A(1,0).点R在y轴上运动,T在x轴上,N为动点,且
如图所示,点A(1,0).点R在y轴上运动,T在x轴上,N为动点,且| RT |
| RA |
| RN |
| RT |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2010•永州一模)如图所示,点A(1,0),B是曲线y=3x2+1上一点,向矩形OABC内随机投一点(该点落在矩形中任一点是等可能的),则所投点落在图中阴影内的概率为( )
(2010•永州一模)如图所示,点A(1,0),B是曲线y=3x2+1上一点,向矩形OABC内随机投一点(该点落在矩形中任一点是等可能的),则所投点落在图中阴影内的概率为( )查看答案和解析>>
科目:高中数学 来源: 题型:单选题
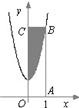 如图所示,点A(1,0),B是曲线y=3x2+1上一点,向矩形OABC内随机投一点(该点落在矩形中任一点是等可能的),则所投点落在图中阴影内的概率为
如图所示,点A(1,0),B是曲线y=3x2+1上一点,向矩形OABC内随机投一点(该点落在矩形中任一点是等可能的),则所投点落在图中阴影内的概率为



查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省茂名市高州市长坡中学高三(下)期初数学试卷(理科)(解析版) 题型:解答题
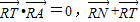 =0,
=0,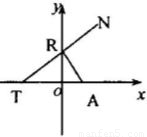
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com