
【题目】已知四面体![]() 中,棱
中,棱![]() ,
,![]() 所在直线所成角为
所在直线所成角为![]() ,且
,且![]() ,
,![]() ,
,![]() ,面
,面![]() 和面
和面![]() 所成的锐二面角为
所成的锐二面角为![]() ,面
,面![]() 和面
和面![]() 所成的锐二面角为
所成的锐二面角为![]() ,当四面体
,当四面体![]() 的体积取得最大值时( ).
的体积取得最大值时( ).
A.![]() B.
B.![]() C.
C.![]() D.不能确定
D.不能确定
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以直角坐标系的原点
为参数).以直角坐标系的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立坐标系,曲线
轴的正半轴为极轴建立坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)若过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,与
两点,与![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年新型冠状病毒肺炎(简称“新冠肺炎”)成为威胁全球的公共卫生问题,中医药在本次新冠肺炎的治疗中发挥了重要作用.研究人员对66例普通型新冠肺炎恢复期患者进行了中医临床特征分析,发现主要证型有气阴两虚证与肺脾气虚证,同时可能兼夹湿证.为研究这两种主要证型在兼夹湿证的难易上是否有差异,研究人员将湿证症状分级量化,将所有肺脾气虚证患者的量化分作成茎叶图.
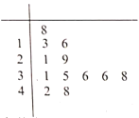
(1)若量化分不低于16分,即可诊断为兼夹湿证,请参考茎叶图,完成下面![]() 列联表.
列联表.
夹湿证 | 非夹湿证 | 合计 | |
气阴两虚 | 20 | ||
肺脾气虚 | |||
合计 | 66 |
(2)根据此资料,能否有99%的把握认为两种主要证型在兼夹湿证的难易上有差异?
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
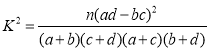
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆P经过点![]() ,并且与圆
,并且与圆![]() 相切.
相切.
(Ⅰ)求圆心P的轨迹C的方程;
(Ⅱ)O是坐标原点,过点![]() 的直线
的直线![]() 与C交于A,B两点,在C上是否存在点Q,使得四边形
与C交于A,B两点,在C上是否存在点Q,使得四边形![]() 是平行四边形?
是平行四边形?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() 为边
为边![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 翻转成
翻转成![]() (
(![]() 平面
平面![]() ).若
).若![]() 分别为线段
分别为线段![]() 的中点,则在
的中点,则在![]() 翻转过程中,下列说法正确的是( )
翻转过程中,下列说法正确的是( )
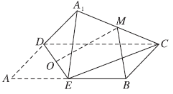
A.与平面![]() 垂直的直线必与直线
垂直的直线必与直线![]() 垂直
垂直
B.异面直线![]() 与
与![]() 所成的角是定值
所成的角是定值
C.一定存在某个位置,使![]()
D.三棱锥![]() 外接球半径与棱
外接球半径与棱![]() 的长之比为定值
的长之比为定值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=ex+asinx,x∈(-π,+∞),下列说法正确的是( )
A.当a=1时,f(x)在(0,f(0))处的切线方程为2x-y+1=0
B.当a=1时,f(x)存在唯一极小值点x0且-1<f(x0)<0
C.对任意a>0,f(x)在(-π,+∞)上均存在零点
D.存在a<0,f(x)在(-π,+∞)上有且只有一个零点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义域均为D的三个函数![]() ,
,![]() ,
,![]() 满足条件:对任意
满足条件:对任意![]() ,点
,点![]() 与点
与点![]() 都关于点
都关于点![]() 对称,则称
对称,则称![]() 是
是![]() 关于
关于![]() 的“对称函数”.已知函数
的“对称函数”.已知函数![]() ,
,![]() ,
,![]() 是
是![]() 关于
关于![]() 的“对称函数“,记
的“对称函数“,记![]() 的定义域为D,若对任意
的定义域为D,若对任意![]() ,都存在
,都存在![]() ,使得
,使得![]() 成立,则实数a的取值范围是( )
成立,则实数a的取值范围是( )
A..![]() B..
B..![]() C..
C..![]() D..
D..![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com