[题目]已知圆O1和圆O2的极坐标方程分别为ρ=2.ρ2-2ρcos(θ-)=2． (1)把圆O1和圆O2的极坐标方程化为直角坐标方程, (2)设两圆交点分别为A.B.求直线AB的参数方程.并利用直线AB的参数方程求两圆的公共弦长|AB|．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知圆O1和圆O2的极坐标方程分别为ρ=2，ρ2-2ρcos（θ-）=2．

（1）把圆O1和圆O2的极坐标方程化为直角坐标方程；

（2）设两圆交点分别为A、B，求直线AB的参数方程，并利用直线AB的参数方程求两圆的公共弦长|AB|．

【答案】（1），；（2）.

【解析】试题分析：（1）利用、把圆，圆的极坐标方程化为直角坐标方程；（2）把2个圆的直角坐标方程相减可得公共弦所在的直线方程，再化为参数方程，利用直线的参数方程求两圆的公共弦长．

试题解析：（1）圆O1的极坐标方程为ρ=2，直角坐标方程，O2的极坐标方程为，ρ2-2ρcos（θ-）=2，直角坐标方程；

（2）两圆的方程相减，可得直线AB的方程为x+y-1=0，参数方程为（t为参数），代入x2+y2=4，可得t2+t-3=0 ，∴|AB|==．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】厂为了对新研发的一种产品进行合理定价，将该产品按事先拟定的价格进行试销，得到如下数据：

单价x/元	8	8.2	8.4	8.6	8.8	9
销量y/件	90	84	83	80	75	68

(1)求线性回归方程=x+，其中=-20， =- .

(2)预计在今后的销售中，销量与单价仍然服从(1)中的关系，且该产品的成本是4元/件，为使工厂获得最大利润，该产品的单价应定为多少元?(利润=销售收入-成本)

查看答案和解析>>

科目：高中数学 来源： 题型：

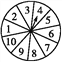
【题目】有一个转盘游戏,转盘被平均分成10等份(如图所示),转动转盘,当转盘停止后,指针指向的数字即为转出的数字.游戏规则如下:两个人参加,先确定猜数方案,甲转动转盘,乙猜,若猜出的结果与转盘转出的数字所表示的特征相符,则乙获胜,否则甲获胜.猜数方案从以下三种方案中选一种:

A.猜“是奇数”或“是偶数”

B.猜“是4的整数倍数”或“不是4的整数倍数”

C.猜“是大于4的数”或“不是大于4的数”

请回答下列问题:

(1)如果你是乙,为了尽可能获胜,你将选择哪种猜数方案,并且怎样猜?为什么?

(2)为了保证游戏的公平性,你认为应制定哪种猜数方案?为什么?

(3)请你设计一种其他的猜数方案,并保证游戏的公平性.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，已知矩形所在平面与底面垂直，在直角梯形中，，， .

(1)求证：平面；

(2)求二面角的大小.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】现从某班的一次期末考试中，随机的抽取了七位同学的数学(满分150分）、物理（满分110分）成绩如下表所示，数学、物理成绩分别用特征量表示，

特征量	1	2	3	4	5	6	7
t	101	124	119	106	122	118	115
y	74	83	87	75	85	87	83

求关于t的回归方程；

（2）利用（1）中的回归方程，分析数学成绩的变化对物理成绩的影响，并估计该班某学生数学成绩130分时，他的物理成绩(精确到个位).

附：回归方程中斜率和截距的最小二乘估计公式分别为：

．

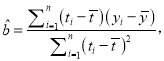
查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】(数学文卷·2017届江西省玉山一中高三上学期第二次月考第16题)中国传统文化中很多内容体现了数学的对称美，如图所示的太极图是由黑白两个鱼形纹组成的圆形图案，充分展现了相互转化、对称统一的形式美、和谐美．给出定义：能够将圆O的周长和面积同时平分的函数称为这个圆的“优美函数”．给出下列命题：①对于任意一个圆O，其“优美函数”有无数个；②函数可以是某个圆的“优美函数”；③正弦函数可以同时是无数个圆的“优美函数”；④函数是“优美函数”的充要条件为函数的图象是中心对称图形．其中正确的命题是__（写出所有正确命题的序号）