
ЎҫМвДҝЎҝҪшИ붬МмЈ¬ҙуЖшБч¶ҜРФұдІоЈ¬ИЭТЧРОіЙОнОХМмЖшЈ¬ҙУ¶шУ°ПмҝХЖшЦКБҝЈ®ДііЗКР»·ұЈІҝГЕКФНјМҪҫҝіөБчБҝУлҝХЖшЦКБҝөДПа№ШРФЈ¬ТФИ·¶ЁКЗ·с¶ФіөБҫКөК©ПЮРРЈ®ОӘҙЛЈ¬»·ұЈІҝГЕІЙјҜөҪёГіЗКР№эИҘТ»ЦЬДЪДіКұ¶ОіөБчБҝУлҝХЖшЦКБҝЦёКэөДКэҫЭИзПВұнЈә

(1)ёщҫЭұнЦРЦЬТ»өҪЦЬОеөДКэҫЭЈ¬Зуy№ШУЪxөДПЯРФ»Ш№й·ҪіМЎЈ
(2)ИфУЙПЯРФ»Ш№й·ҪіМөГөҪөД№АјЖКэҫЭУлЛщСЎіцөДјмСйКэҫЭөДОуІоҫщІ»і¬№э2Ј¬ФтИПОӘөГөҪөДПЯРФ»Ш№й·ҪіМКЗҝЙҝҝөДЈ®ЗлёщҫЭЦЬБщәНЦЬИХКэҫЭЈ¬ЕР¶ЁЛщөГөДПЯРФ»Ш№й·ҪіМКЗ·сҝЙҝҝЈҝ
ЧўЈә»Ш№й·ҪіМ![]() ЦРРұВКәНҪШҫаЧоРЎ¶юіЛ№АјЖ№«КҪ·ЦұрОӘ
ЦРРұВКәНҪШҫаЧоРЎ¶юіЛ№АјЖ№«КҪ·ЦұрОӘ .
.
Ўҫҙр°ёЎҝЈЁ1Ј©![]() Ј»ЈЁ2Ј©ҝЙҝҝ.
Ј»ЈЁ2Ј©ҝЙҝҝ.
ЎҫҪвОцЎҝ
ЈЁ1Ј©ёщҫЭЛщёшөДКэҫЭЈ¬ЗуіцxЈ¬yөДЖҪҫщКэЈ¬ёщҫЭЗуПЯРФ»Ш№й·ҪіМПөКэөД·Ҫ·ЁЈ¬ЗуіцПөКэ![]() Ј¬°С
Ј¬°С![]() әНxЈ¬yөДЖҪҫщКэЈ¬ҙъИлЗу
әНxЈ¬yөДЖҪҫщКэЈ¬ҙъИлЗу![]() өД№«КҪЈ¬Зуіц
өД№«КҪЈ¬Зуіц![]() өДЦөЈ¬јҙҝЙөГПЯРФ»Ш№й·ҪіМЈ®
өДЦөЈ¬јҙҝЙөГПЯРФ»Ш№й·ҪіМЈ®
ЈЁ2Ј©ёщҫЭЛщЗуөДПЯРФ»Ш№й·ҪіМЈ¬ФӨұЁөұЧФұдБҝОӘ8әН8.5КұөДyөДЦөЈ¬°СФӨұЁөДЦөН¬ФӯАҙұнЦРЛщёшөД8әН8.5¶ФУҰөДЦөЧцІоЈ¬ІоөДҫш¶ФЦөІ»і¬№э2Ј¬өГөҪПЯРФ»Ш№й·ҪіМҝЙҝҝЈ®
ЈЁ1Ј©![]() Ј¬
Ј¬![]() Ј®
Ј®
Ўа 
![]() =5Ј¬
=5Ј¬
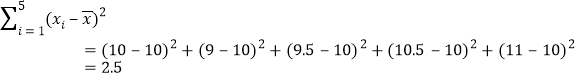 Ј¬Ўа
Ј¬Ўа  Ј®Ўа
Ј®Ўа ![]() Ўа y№ШУЪxөДПЯРФ»Ш№й·ҪіМОӘ
Ўа y№ШУЪxөДПЯРФ»Ш№й·ҪіМОӘ![]() .
.
ЈЁ2Ј©өұx=8КұЈ¬![]() Ј®ВъЧг|74-73|=1<2Ј¬өұx=8.5КұЈ¬
Ј®ВъЧг|74-73|=1<2Ј¬өұx=8.5КұЈ¬![]() Ј®ВъЧг|75-75|=0<2Ј¬Ўа ЛщөГөДПЯРФ»Ш№й·ҪіМКЗҝЙҝҝөДЈ®
Ј®ВъЧг|75-75|=0<2Ј¬Ўа ЛщөГөДПЯРФ»Ш№й·ҪіМКЗҝЙҝҝөДЈ®



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘ¶ЁТеФЪ![]() ЙПөДәҜКэ
ЙПөДәҜКэ![]() ЗТІ»әгОӘБгЈ¬¶Ф
ЗТІ»әгОӘБгЈ¬¶Ф![]() ВъЧг
ВъЧг![]() Ј¬ЗТ
Ј¬ЗТ![]() ФЪ
ФЪ![]() ЙПөҘөчөЭФцЈ®
ЙПөҘөчөЭФцЈ®
ЈЁ1Ј©Зу![]() Ј¬
Ј¬![]() өДЦөЈ¬ІўЕР¶ПәҜКэ
өДЦөЈ¬ІўЕР¶ПәҜКэ![]() өДЖжЕјРФЈ»
өДЖжЕјРФЈ»
ЈЁ2Ј©Зу![]() өДҪвјҜЈ®
өДҪвјҜЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘНЦФІ![]() өДУТҪ№өгОӘ
өДУТҪ№өгОӘ![]() ,ЧшұкФӯөгОӘ
,ЧшұкФӯөгОӘ![]() .НЦФІ
.НЦФІ![]() өД¶ҜПТ
өД¶ҜПТ![]() №эУТҪ№өг
№эУТҪ№өг![]() ЗТІ»ҙ№ЦұУЪЧшұкЦбЈ¬
ЗТІ»ҙ№ЦұУЪЧшұкЦбЈ¬![]() өДЦРөгОӘ
өДЦРөгОӘ![]() ,№э
,№э![]() ЗТҙ№ЦұУЪПЯ¶О
ЗТҙ№ЦұУЪПЯ¶О![]() өДЦұПЯҪ»ЙдПЯ
өДЦұПЯҪ»ЙдПЯ![]() УЪөг
УЪөг![]() .
.
(I)Зуөг![]() өДәбЧшұк;
өДәбЧшұк;
(II)өұ![]() ЧоҙуКұЈ¬Зу
ЧоҙуКұЈ¬Зу![]() өДГж»э.
өДГж»э.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИэ№ъКұЖЪХФЛ¬ФЪЎ¶№ҙ№Й·ҪФІНјЧўЎ·ЦРЈ¬¶Ф№ҙ№Й¶ЁАнөДЦӨГчҝЙУГПЦҙъКэС§ұнКцОӘИзНјЛщКҫЈ¬ОТГЗҪМІДЦРАыУГёГНјЧчОӘјёәОҪвКНөДКЗЈЁ Ј©

A.Из№ы![]() Ј¬ДЗГҙ
Ј¬ДЗГҙ![]()
B.Из№ы![]() Ј¬ДЗГҙ
Ј¬ДЗГҙ![]()
C.Из№ы![]() Ј¬ДЗГҙ
Ј¬ДЗГҙ![]()
D.¶ФИОТвКөКэ![]() әН
әН![]() Ј¬УР
Ј¬УР![]() Ј¬өұЗТҪцөұ
Ј¬өұЗТҪцөұ![]() КұЈ¬өИәЕіЙБў
КұЈ¬өИәЕіЙБў
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝ¶ЁТеФЪRЙПөДәҜКэfЈЁxЈ©ЈҪ|x2©Ғax|ЈЁaЎКRЈ©Ј¬ЙиgЈЁxЈ©ЈҪfЈЁx+lЈ©©ҒfЈЁxЈ©.
ЈЁ1Ј©ИфyЈҪgЈЁxЈ©ОӘЖжәҜКэЈ¬ЗуaөДЦөЈә
ЈЁ2Ј©ЙиhЈЁxЈ©![]() Ј¬xЎКЈЁ0Ј¬+ЎЮЈ©
Ј¬xЎКЈЁ0Ј¬+ЎЮЈ©
ўЩИфaЎЬ0Ј¬ЦӨГчЈәhЈЁxЈ©Јҫ2Јә
ўЪИфhЈЁxЈ©өДЧоРЎЦөОӘ©Ғ1Ј¬ЗуaөДИЎЦө·¶О§.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝ[СЎРЮ4-5ЈәІ»өИКҪСЎҪІ]
ТСЦӘәҜКэ![]() .
.
ЈЁўсЈ©өұ![]() КұЈ¬Зу
КұЈ¬Зу![]() өДҪвјҜЈ»
өДҪвјҜЈ»
ЈЁўтЈ©өұ![]() КұЈ¬
КұЈ¬ ![]() әгіЙБўЈ¬ЗуКөКэ
әгіЙБўЈ¬ЗуКөКэ![]() өДИЎЦө·¶О§.
өДИЎЦө·¶О§.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘәҜКэ![]() ,ЗТЗъПЯ
,ЗТЗъПЯ![]() ФЪөг
ФЪөг![]() ҙҰөДЗРПЯУл
ҙҰөДЗРПЯУл![]() Цбҙ№Цұ.
Цбҙ№Цұ.
(I)ЗуәҜКэ![]() өДөҘөчЗшјд;
өДөҘөчЗшјд;
(ўт)Иф¶ФИОТв![]() (ЖдЦР
(ЖдЦР![]() ОӘЧФИ»¶ФКэөДөЧКэ),¶јУР
ОӘЧФИ»¶ФКэөДөЧКэ),¶јУР![]() әгіЙБў,Зу
әгіЙБў,Зу![]() өДИЎЦө·¶О§.
өДИЎЦө·¶О§.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝ2019ДклшЦЭДіЖуТөјЖ»®ТэҪшРВДЬФҙЖыіөЙъІъЙиұёЈ¬НЁ№эКРіЎ·ЦОцЈ¬И«ДкРиН¶Ил№М¶ЁіЙұҫ2500НтФӘ.ГҝЙъІъ![]() ЈЁ°ЩБҫЈ©РВДЬФҙЖыіөЈ¬РиБнН¶ИліЙұҫ
ЈЁ°ЩБҫЈ©РВДЬФҙЖыіөЈ¬РиБнН¶ИліЙұҫ![]() НтФӘЈ¬ЗТ
НтФӘЈ¬ЗТ .УЙКРіЎөчСРЦӘЈ¬ГҝБҫіөКЫјЫ5НтФӘЈ¬ЗТЙъІъөДіөБҫөұДкДЬИ«ІҝПъКЫНк.
.УЙКРіЎөчСРЦӘЈ¬ГҝБҫіөКЫјЫ5НтФӘЈ¬ЗТЙъІъөДіөБҫөұДкДЬИ«ІҝПъКЫНк.
ЈЁ1Ј©Зуіц2019ДкөДАыИу![]() ЈЁНтФӘЈ©№ШУЪДкІъБҝ
ЈЁНтФӘЈ©№ШУЪДкІъБҝ![]() ЈЁ°ЩБҫЈ©өДәҜКэ№ШПөКҪЈ»ЈЁАыИу=ПъКЫ-іЙұҫЈ©
ЈЁ°ЩБҫЈ©өДәҜКэ№ШПөКҪЈ»ЈЁАыИу=ПъКЫ-іЙұҫЈ©
ЈЁ2Ј©2019ДкІъБҝОӘ¶аЙЩ°ЩБҫКұЈ¬ЖуТөЛщ»сАыИуЧоҙуЈҝІўЗуіцЧоҙуАыИу.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝЈЁМвОДЈ©ИзНјЈ¬ФЪОеГжМеABCDEFЦРЈ¬ЛДұЯРОEDCFКЗХэ·ҪРОЈ¬![]() Ј®
Ј®

(1)ЦӨГчЈә![]() Ј»
Ј»
(2)ТСЦӘЛДұЯРОABCDКЗөИСьМЭРОЈ¬ЗТ![]() Ј¬ЗуОеГжМеABCDEFөДМе»э.
Ј¬ЗуОеГжМеABCDEFөДМе»э.
Ійҝҙҙр°ёәНҪвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com