
分析 写出命题的否定判断①;由函数的奇偶性的性质判断②;求出复合函数的值域判断③;由函数的单调性与导函数间的关系判断④;由已知等式求得f(x+8)=f(x),再由周期概念判断⑤.
解答 解:①、命题“?x∈R,cosx>0”的否定是“?x∈R,cosx≤0”,故①错误;
②、若y=f(x)是奇函数,则y=|f(x)|为偶函数,其图象关于y轴对称,故②正确;
③、∵3x>0,∴1-3x<1,则函数f(x)=log2(1-3x)的值域为(-∞,0),故③正确;
④、对任意实数x,有f(-x)=f(x),可知函数f(x)为偶函数,当x>0时,f′(x)>0,函数为增函数,则当x<0时,函数为减函数,有f′(x)<0,故④正确;
⑤、若函数f(x)对任意x∈R满足f(x)•f(x+4)=1,则f(x+4)=$\frac{1}{f(x)}$,∴f(x+8)=$\frac{1}{f(x+4)}=\frac{1}{\frac{1}{f(x)}}=f(x)$,8是函数f(x)的一个周期,故⑤正确.
∴其中的真命题是②③④⑤.
故答案为:②③④⑤.
点评 本题考查命题的真假判断与应用,考查函数的性质,考查全称命题的否定,是中档题.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
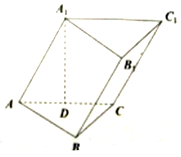 如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1是边长为4的菱形,BC⊥平面ACC1A1,CB=2,点A1在底面ABC上的射影D为棱AC的中点,点A在平面A1CB内的射影为E.
如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1是边长为4的菱形,BC⊥平面ACC1A1,CB=2,点A1在底面ABC上的射影D为棱AC的中点,点A在平面A1CB内的射影为E.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com