
【题目】已知函数![]() .
.
(Ⅰ)若函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求
,求![]() 和
和![]() 的值;
的值;
(Ⅱ)讨论方程![]() 的解的个数,并说明理由.
的解的个数,并说明理由.
【答案】(1) ![]() ,
, ![]() ;(2)当
;(2)当![]() 时,方程无解;当
时,方程无解;当![]() 或
或![]() 时,方程有唯一解;当
时,方程有唯一解;当![]() 时,方程
时,方程![]() 有两解.
有两解.
【解析】试题分析: (Ⅰ)求出导函数,利用![]() 在处的切线方程为
在处的切线方程为![]() ,列出方程组求解
,列出方程组求解![]() ;(Ⅱ)通过
;(Ⅱ)通过![]() ,判断方程的解
,判断方程的解![]() 出函数的导数判断函数的单调性,求出极小值,分析出当
出函数的导数判断函数的单调性,求出极小值,分析出当![]()
![]() 时,方程无解;当
时,方程无解;当![]() 或
或![]() 时,方程有唯一解;当
时,方程有唯一解;当![]() 时,方程有两解.
时,方程有两解.
试题解析:(Ⅰ)因为![]() ,又
,又![]() 在
在![]() 处得切线方程为
处得切线方程为![]() ,
,
所以![]() ,解得
,解得![]() .
.
(Ⅱ)当![]() 时,
时, ![]() 在定义域
在定义域![]() 内恒大于0,此时方程无解.
内恒大于0,此时方程无解.
当![]() 时,
时, ![]() 在区间
在区间![]() 内恒成立,
内恒成立,
所以![]() 为定义域为增函数,因为
为定义域为增函数,因为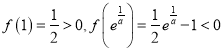 ,
,
所以方程有唯一解.
当![]() 时,
时, ![]() .
.
当![]() 时,
时, ![]() ,
, ![]() 在区间
在区间![]() 内为减函数,
内为减函数,
当![]() 时,
时, ![]() ,
, ![]() 在区间
在区间![]() 内为增函数,
内为增函数,
所以当![]() 时,取得最小值
时,取得最小值![]() .
.
当![]() 时,
时, ![]() ,无方程解;
,无方程解;
当![]() 时,
时, ![]() ,方程有唯一解.
,方程有唯一解.
当![]() 时,
时, ![]() ,
,
因为![]() ,且
,且![]() ,所以方程
,所以方程![]() 在区间
在区间![]() 内有唯一解,
内有唯一解,
当![]() 时,设
时,设![]() ,所以
,所以![]() 在区间
在区间![]() 内为增函数,
内为增函数,
又![]() ,所以
,所以![]() ,即
,即![]() ,故
,故![]() .
.
因为![]() ,所以
,所以![]() .
.
所以方程![]() 在区间
在区间![]() 内有唯一解,所以方程
内有唯一解,所以方程![]() 在区间
在区间![]() 内有两解,
内有两解,
综上所述,当![]() 时,方程无解.
时,方程无解.


科目:高中数学 来源: 题型:
【题目】某养殖厂需定期购买饲料,已知该厂每天需要饲料200 kg,每千克饲料的价格为1.8元,饲料的保管与其他费用为平均每千克每天0.03元,购买饲料每次支付运费300元.
(1)该厂多少天购买一次饲料才能使平均每天支付的总费用最少?
(2)若提供饲料的公司规定:当一次购买饲料不少于5 t时其价格可享受八五折优惠(即为原价的85%).该厂是否可以考虑利用此优惠条件?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角坐标系![]() 中,O为坐标原点.动点P在圆
中,O为坐标原点.动点P在圆![]() 上,过P作y轴的垂线,垂足为N,点M在射线NP上,满足
上,过P作y轴的垂线,垂足为N,点M在射线NP上,满足![]() .
.

(1)求点M的轨迹G的方程;
(2)过点![]() 的直线l交轨迹G 于A,B两点,交圆O于C,D两点.若
的直线l交轨迹G 于A,B两点,交圆O于C,D两点.若![]() ,求直线l的方程;
,求直线l的方程;
(3)设点Q(3, t)(t∈R,t ≠ 0),且![]() ,过点P且垂直于OQ的直线m与OQ交于点E,与x轴交于点F,求△OEF周长最大时的直线m的方程.
,过点P且垂直于OQ的直线m与OQ交于点E,与x轴交于点F,求△OEF周长最大时的直线m的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,设内角A,B,C所对边分别为a,b,c,且sin(A﹣ ![]() )﹣cos(A+
)﹣cos(A+ ![]() )=
)= ![]() .
.
(1)求角A的大小;
(2)若a= ![]() ,sin2B+cos2C=1,求△ABC的面积.
,sin2B+cos2C=1,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣2ax(其中a∈R).
(Ⅰ)当a=1时,求函数f(x)的图象在x=1处的切线方程;
(Ⅱ)若f(x)≤1恒成立,求a的取值范围;
(Ⅲ)设g(x)=f(x)+ ![]() x2 , 且函数g(x)有极大值点x0 , 求证:x0f(x0)+1+ax02>0.
x2 , 且函数g(x)有极大值点x0 , 求证:x0f(x0)+1+ax02>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如下图).由图中数据可知a=________,估计该小学学生身高的中位数为______

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的三个顶点
的三个顶点![]() ,其外接圆为圆
,其外接圆为圆![]() .
.
(1)若直线![]() 过点
过点![]() ,且被圆
,且被圆![]() 截得的弦长为
截得的弦长为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)对于线段![]() (包括端点)上的任意一点
(包括端点)上的任意一点![]() ,若在以
,若在以![]() 为圆心的圆上都存在不同的两点
为圆心的圆上都存在不同的两点![]() ,使得点
,使得点![]() 是线段
是线段![]() 的中点,求圆
的中点,求圆![]() 的半径
的半径![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-5:不等式选讲
已知函数f(x)=4﹣|x|﹣|x﹣3|
(Ⅰ)求不等式f(x+ ![]() )≥0的解集;
)≥0的解集;
(Ⅱ)若p,q,r为正实数,且 ![]() =4,求3p+2q+r的最小值.
=4,求3p+2q+r的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com