
���� ��1��ÿ���Ӯ��ΪT=�ղ�����x������Ʒ�ʣ�1-P����2-�ղ�����x������Ʒ�ʣ�P����1�����ݷֶκ����ֶ��о����������ɣ�
��2�����û�������ʽ���������ֵ��
��� �⣺��1����x��6ʱ��P=$\frac{2}{3}$����T=$\frac{1}{3}$x��2-$\frac{2}{3}$x��1=0��
��1��x��6ʱ��P=$\frac{1}{6-x}$����T=��1-$\frac{1}{6-x}$��x��2-��$\frac{1}{6-x}$��x��1=$\frac{9x-2{x}^{2}}{6-x}$��
������������ӯ����T����Ԫ�����ղ���x��������ĺ�����ϵΪ��T=$\left\{\begin{array}{l}{\frac{9x-2{x}^{2}}{6-x}��1��x��6}\\{0��x��6}\end{array}\right.$������6�֣�
��2���ɣ�1��֪����x��6ʱ��ÿ���ӯ��Ϊ0��
��1��x��6ʱ��T��x��=$\frac{9x-2{x}^{2}}{6-x}$=15-2[��6-x��+$\frac{9}{6-x}$]��15-12=3��
��T��3��
���ҽ���x=3ʱ��T=3��
���ϣ����ղ���Ϊ3���ʱ���ɻ���������3��Ԫ������12�֣�
���� ���⿼����������ģ�͵�Ӧ�ã��������û�������ʽ��ú�������ֵ���⣬Ҳ�����˷ֶκ��������⣬��������˼�룮���е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | -1 | C�� | 9 | D�� | 10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {0��1��2��2} | B�� | {0��1��2} | C�� | {0} | D�� | {0��1} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [-3��2�� | B�� | [-3��2] | C�� | ��-1��2�� | D�� | ��-1��2] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
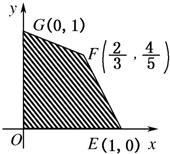 ��ͼ��Ŀ�꺯��z=kx-y�Ŀ�����Ϊ�ı���OEFG�����߽磩������F��$\frac{2}{3}$��$\frac{4}{5}$����Ŀ�꺯�������Ž⣬��k��ȡֵ��Χ�ǣ�������
��ͼ��Ŀ�꺯��z=kx-y�Ŀ�����Ϊ�ı���OEFG�����߽磩������F��$\frac{2}{3}$��$\frac{4}{5}$����Ŀ�꺯�������Ž⣬��k��ȡֵ��Χ�ǣ�������| A�� | ��-$\frac{12}{5}$��$\frac{4}{5}$�� | B�� | ��$\frac{3}{10}��\frac{12}{5}$�� | C�� | [-$\frac{12}{5}$��-$\frac{3}{10}$] | D�� | [-$\frac{3}{10}$��-$\frac{12}{5}$] |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com