
【题目】已知定义域为R的函数f(x)= ![]() 是奇函数.
是奇函数.
(1)求a,b的值;
(2)判断函数f(x)的单调性,并用定义证明;
(3)若对于任意 ![]() 都有f(kx2)+f(2x﹣1)>0成立,求实数k的取值范围.
都有f(kx2)+f(2x﹣1)>0成立,求实数k的取值范围.
【答案】
(1)解:因为f(x)是奇函数,所以f(0)=0 ![]() =0,解得b=1,
=0,解得b=1,
f(x)= ![]() ,又由f(1)=﹣f(﹣1)
,又由f(1)=﹣f(﹣1) ![]() ,解得a=2
,解得a=2
(2)证明:由(1)可得:f(x)= ![]() =
= ![]() .
.
x1<x2,∴ ![]() >0,
>0,
则f(x1)﹣f(x2)= ![]() =
= ![]() >0,
>0,
∴f(x1)>f(x2).
∴f(x)在R上是减函数
(3)解:∵函数f(x)是奇函数.
∴f(kx2)+f(2x﹣1)>0成立,等价于f(kx2)>﹣f(2x﹣1)=f(1﹣2x)成立,
∵f(x)在R上是减函数,∴kx2<1﹣2x,
∴对于任意 ![]() 都有kx2<1﹣2x成立,
都有kx2<1﹣2x成立,
∴对于任意 ![]() 都有k<
都有k< ![]() ,
,
设g(x)= ![]() ,
,
∴g(x)= ![]() =
= ![]() ,
,
令t= ![]() ,t∈[
,t∈[ ![]() ,2],
,2],
则有 ![]() ,∴g(x)min=g(t)min=g(1)=﹣1
,∴g(x)min=g(t)min=g(1)=﹣1
∴k<﹣1,即k的取值范围为(﹣∞,﹣1)
【解析】(1)直接根据函数是奇函数,满足f(﹣x)=﹣f(x),把x=0,和x=1代入,即可得到关于a,b的两个等式,解方程组求出a,b的值.(2)利用减函数的定义即可证明.(3))f(kx2)+f(2x﹣1)>0成立,等价于f(kx2)>﹣f(2x﹣1)=f(1﹣2x),即k< ![]() 成立,设g(x)=
成立,设g(x)= ![]() ,
,
换元使之成为二次函数,再求最小值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】把正方形AA1B1B以边AA1所在直线为轴旋转900到正方形AA1C1C,其中D,E,F分别为B1A,C1C,BC的中点. 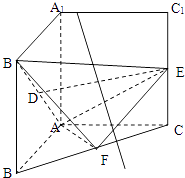
(1)求证:DE∥平面ABC;
(2)求证:B1F⊥平面AEF;
(3)求二面角A﹣EB1﹣F的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国移动通信公司早前推出“全球通”移动电话资费“个性化套餐”,具体方案如下:
方案代号 | 基本月租(元) | 免费时间(分钟) | 超过免费时间的话费(元/分钟) |
1 | 30 | 48 | 0.60 |
2 | 98 | 170 | 0.60 |
3 | 168 | 330 | 0.50 |
4 | 268 | 600 | 0.45 |
5 | 388 | 1000 | 0.40 |
6 | 568 | 1700 | 0.35 |
7 | 788 | 2588 | 0.30 |
(I)写出“套餐”中方案![]() 的月话费
的月话费![]() (元)与月通话量
(元)与月通话量![]() (分钟)(月通话量是指一个月内每次通话用时之和)的函数关系式;
(分钟)(月通话量是指一个月内每次通话用时之和)的函数关系式;
(II)学生甲选用方案![]() ,学生乙选用方案
,学生乙选用方案![]() ,某月甲乙两人的电话资费相同,通话量也相同,求该月学生甲的电话资费;
,某月甲乙两人的电话资费相同,通话量也相同,求该月学生甲的电话资费;
(III)某用户的月通话量平均为320分钟,则在表中所列出的七种方案中,选择哪种方案更合算,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,正确的是 .
①任取x>0,均有3x>2x;
②当a>0,且a≠1时,有a3>a2;
③y=( ![]() )﹣x是减函数;
)﹣x是减函数;
④函数f(x)在x>0时是增函数,x<0也是增函数,所以f(x)是增函数;
⑤若函数f(x)=ax2+bx+2与x轴没有交点,则b2﹣8a<0且a>0;
⑥y=x2﹣2|x|﹣3的递增区间为[1,+∞).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商品最近30天的价格f(t)(元)与时间t满足关系式:f(t)=  ,且知销售量g(t)与时间t满足关系式 g(t)=﹣t+30,(0≤t≤30,t∈N+),求该商品的日销售额的最大值.
,且知销售量g(t)与时间t满足关系式 g(t)=﹣t+30,(0≤t≤30,t∈N+),求该商品的日销售额的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出的以下四个问题中,不需要用条件语句来描述其算法是( )
A.输入一个实数x,求它的绝对值
B.求面积为6的正方形的周长
C.求三个数a、b、c中的最大数
D.求函数f(x)= ![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x|x+2<0},B={x|(x+3)(x﹣1)>0}.
(1)求集合A∩B;
(2)若不等式ax2+2x+b>0的解集为A∪B,求a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H,则以下命题中,错误的命题是( ) 
A.点H是△A1BD的垂心
B.AH垂直平面CB1D1
C.AH的延长线经过点C1
D.直线AH和BB1所成角为45°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com