
【题目】如图(1),在等腰直角![]() 中,斜边
中,斜边![]() ,D为
,D为![]() 的中点,将
的中点,将![]() 沿
沿![]() 折叠得到如图(2)所示的三棱锥
折叠得到如图(2)所示的三棱锥![]() ,若三棱锥
,若三棱锥![]() 的外接球的半径为
的外接球的半径为![]() ,则
,则![]() _________.
_________.
图(1)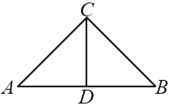 图(2)
图(2) 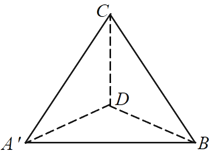
【答案】![]()
【解析】
根据题意,先找到球心的位置,再根据球的半径是![]() ,以及已有的边的长度和角度关系,分析即可解决.
,以及已有的边的长度和角度关系,分析即可解决.
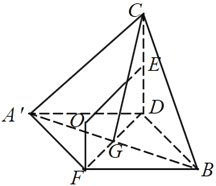
解:球是三棱锥C﹣A'BD的外接球,所以球心O到各顶点的距离相等,如图.
根据题意,CD⊥平面A'BD,
取CD的中点E,A'B的中点G,连接CG,DG,
因为A'D=BD,CD⊥平面A'BD,
所以A'和B关于平面CDG对称,
在平面CDG内,作线段CD的垂直平分线,则球心O在线段CD的垂直平分线上,设为图中的O点位置,过
O作直线CD的平行线,交平面A'BD于点F,
则OF⊥平面A'BD,且OF=DE=1,
因为A'F在平面A'BD内,所以OF⊥A'F,
即三角形A'OF为直角三角形,且斜边OA'=R![]() ,
,
∴A'F![]() 2,
2,
所以,BF=2,
所以四边形A'DBF为菱形,
又知OD=R,三角形ODE为直角三角形,
∴OE![]() 2,
2,
∴三角形A'DF为等边三角形,
∴∠A'DF![]() ,
,
故∠A'DB![]() ,
,
故填:![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点为
的左焦点为![]() ,设
,设![]() ,
,![]() 是椭圆
是椭圆![]() 的两个短轴端点,
的两个短轴端点,![]() 是椭圆
是椭圆![]() 的长轴左端点.
的长轴左端点.
(1)当![]() 时,设点
时,设点![]() ,
,![]() ,直线
,直线![]() 交椭圆
交椭圆![]() 于
于![]() ,且直线
,且直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,求
,求![]() 的值;
的值;
(2)当![]() 时,若经过
时,若经过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 为坐标原点,求
为坐标原点,求![]() 与
与![]() 的面积之差的最大值.
的面积之差的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为![]()
![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,取相同的长度单位建立极坐标系,曲线
轴的非负半轴为极轴,取相同的长度单位建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 上的点到直线l的最大距离为
上的点到直线l的最大距离为![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在我们的教材必修一中有这样一个问题,假设你有一笔资金,现有三种投资方案供你选择,这三种方案的回报如下:
方案一:每天回报![]() 元;
元;
方案二:第一天回报![]() 元,以后每天比前一天多回报
元,以后每天比前一天多回报![]() 元;
元;
方案三:第一天回报![]() 元,以后每天的回报比前一天翻一番.
元,以后每天的回报比前一天翻一番.
记三种方案第![]() 天的回报分别为
天的回报分别为![]() ,
,![]() ,
,![]() .
.
(1)根据数列的定义判断数列![]() ,
,![]() ,
,![]() 的类型,并据此写出三个数列的通项公式;
的类型,并据此写出三个数列的通项公式;
(2)小王准备做一个为期十天的短期投资,他应该选择哪一种投资方案?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为践行“绿水青山就是金山银山”的发展理念和提高生态环境的保护意识,高二年级准备成立一个环境保护兴趣小组.该年级理科班有男生400人,女生200人;文科班有男生100人,女生300人.现按男、女用分层抽样从理科生中抽取6人,按男、女分层抽样从文科生中抽取4人,组成环境保护兴趣小组,再从这10人的兴趣小组中抽出4人参加学校的环保知识竞赛.
(1)设事件![]() 为“选出的这4个人中要求有两个男生两个女生,而且这两个男生必须文、理科生都有”,求事件
为“选出的这4个人中要求有两个男生两个女生,而且这两个男生必须文、理科生都有”,求事件![]() 发生的概率;
发生的概率;
(2)用![]() 表示抽取的4人中文科女生的人数,求
表示抽取的4人中文科女生的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知球O是正三棱锥(底面为正三角形,顶点在底面的射影为底面中心)A-BCD的外接球,BC=3,![]() ,点E在线段BD上,且BD=3BE,过点E作圆O的截面,则所得截面圆面积的取值范围是__.
,点E在线段BD上,且BD=3BE,过点E作圆O的截面,则所得截面圆面积的取值范围是__.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点为极点,x轴的非负半轴为极轴,建立极坐标系,并在两种坐标系中取相同的长度单位,已知直线l的参数方程为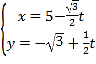 (t为参数),圆C的极坐标方程为
(t为参数),圆C的极坐标方程为![]()
(1)求直线l和圆C的直角坐标方程;
(2)若点![]() 在圆C上,求
在圆C上,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由于浓酸泄漏对河流形成了污染,现决定向河中投入固体碱,1个单位的固体碱在水中逐步溶化,水中的碱浓度![]() 与时间
与时间![]() 的关系,可近似地表示为
的关系,可近似地表示为 ,只有当河流中碱的浓度不低于1时,才能对污染产生有效的抑制作用.
,只有当河流中碱的浓度不低于1时,才能对污染产生有效的抑制作用.
(1)如果只投放1个单位的固体碱,则能够维持有效抑制作用的时间有多长?
(2)当河中的碱浓度开始下降时,即刻第二次投放1个单位的固体碱,此后,每一时刻河中的碱浓度认为是各次投放的碱在该时刻相应的碱浓度的和,求河中碱浓度可能取得的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线外一点M作抛物线的两条切线,两切点的连线段称为点M对应的切点弦已知抛物线为![]() ,点P,Q在直线l:
,点P,Q在直线l:![]() 上,过P,Q两点对应的切点弦分别为AB,CD
上,过P,Q两点对应的切点弦分别为AB,CD
![]() 当点P在l上移动时,直线AB是否经过某一定点,若有,请求出该定点的坐标;如果没有,请说明理由
当点P在l上移动时,直线AB是否经过某一定点,若有,请求出该定点的坐标;如果没有,请说明理由
![]() 当
当![]() 时,点P,Q在什么位置时,
时,点P,Q在什么位置时,![]() 取得最小值?
取得最小值?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com