
| A. | $\frac{1}{3}•{(\frac{1}{2})^{n-1}}$ | B. | $\frac{1}{2}•{(\frac{2}{3})^{n-1}}$ | C. | $2•{(\frac{1}{3})^n}-\frac{1}{3}$ | D. | ${(\frac{1}{3})^n}$ |
分析 由已知数列递推式求出首项,进一步得到${a}_{n}=\frac{1}{3}{a}_{n-1}$(n≥2).可得数列{an}是以$\frac{1}{3}$为首项,以$\frac{1}{3}$为公比的等比数列,代入等比数列的通项公式得答案.
解答 解:由${S_n}=\frac{1}{2}-\frac{1}{2}{a_n}$,取n=1,得${a}_{1}={S}_{1}=\frac{1}{2}-\frac{1}{2}{a}_{1}$,即${a}_{1}=\frac{1}{3}$.
当n≥2时,an=Sn-Sn-1=$\frac{1}{2}-\frac{1}{2}{a}_{n}-(\frac{1}{2}-\frac{1}{2}{a}_{n-1})$,
即${a}_{n}=\frac{1}{3}{a}_{n-1}$(n≥2).
∴数列{an}是以$\frac{1}{3}$为首项,以$\frac{1}{3}$为公比的等比数列,
则${a}_{n}=\frac{1}{3}•(\frac{1}{3})^{n-1}=(\frac{1}{3})^{n}$.
故选:D.
点评 本题考查数列递推式,考查了等比关系的确定,训练了等比数列通项公式的求法,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{12}$ | B. | 向右平移$\frac{π}{12}$ | C. | 向左平移$\frac{π}{6}$ | D. | 向右平移$\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“?x>1,x2-1>0”的否定是“?x>1,x2-1≤0” | |
| B. | “x=2”是“x2-x-2=0”的充分不必要条件 | |
| C. | 若“p∧q”为假命题,则p,q均为假命题 | |
| D. | 命题“若a•b=0,则a=0或b=0”的否命题为“若a•b≠0,则a≠0且b≠0” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
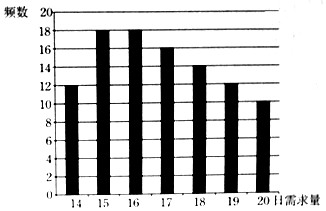 某蛋糕店每天制作生日蛋糕若干个,每个生日蛋糕成本为50元,每个蛋糕的售价为100元,如果当天卖不完,剩余的蛋糕作垃圾处理.现搜集并整理了100天生日蛋糕的日需求量(单位:个),得到如图所示的柱状图.100天记录的各需求量的频率作为每天各需求量发生的概率.
某蛋糕店每天制作生日蛋糕若干个,每个生日蛋糕成本为50元,每个蛋糕的售价为100元,如果当天卖不完,剩余的蛋糕作垃圾处理.现搜集并整理了100天生日蛋糕的日需求量(单位:个),得到如图所示的柱状图.100天记录的各需求量的频率作为每天各需求量发生的概率.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
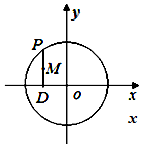 如图,在圆x2+y2=16上任取一点P,过点P作x 轴的垂线段PD,D为垂足,当点P在圆上运动时,则线段PD的中点M的轨迹方程为$\frac{x^2}{16}+\frac{y^2}{4}=1$.
如图,在圆x2+y2=16上任取一点P,过点P作x 轴的垂线段PD,D为垂足,当点P在圆上运动时,则线段PD的中点M的轨迹方程为$\frac{x^2}{16}+\frac{y^2}{4}=1$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com