
【题目】已知![]() (
(![]() 且
且![]() )是R上的奇函数,且
)是R上的奇函数,且![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)若关于x的方程![]() 在区间
在区间![]() 内只有一个解,求m的取值集合;
内只有一个解,求m的取值集合;
(3)设![]() ,记
,记![]() ,是否存在正整数n,使不得式
,是否存在正整数n,使不得式![]() 对一切
对一切![]() 均成立?若存在,求出所有n的值,若不存在,说明理由.
均成立?若存在,求出所有n的值,若不存在,说明理由.
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求![]() 的极值;
的极值;
(2)若函数![]() 在定义域内为增函数,求实数
在定义域内为增函数,求实数![]() 的取值范围;
的取值范围;
(3)设![]() ,若函数
,若函数![]() 存在两个零点
存在两个零点![]() ,且满足
,且满足![]() ,问:函数
,问:函数![]() 在
在![]() 处的切线能否平行于
处的切线能否平行于![]() 轴?若能,求出该切线方程,若不能,请说明理由.
轴?若能,求出该切线方程,若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为内角A,B,C的对边,且2asinA=(2b-c)sinB+(2c-b)sinC..
(1)求角A的大小;
(2)若sinB+sinC=![]() ,试判断△ABC的形状.
,试判断△ABC的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于随机变量及分布的说法正确的是( )
A.抛掷均匀硬币一次,出现正面的次数是随机变量
B.某人射击时命中的概率为0.5,此人射击三次命中的次数![]() 服从两点分布
服从两点分布
C.离散型随机变量的分布列中,随机变量取各个值的概率之和可以小于1
D.离散型随机变量的各个可能值表示的事件是彼此互斥的
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在工业生产中,对一正三角形薄钢板(厚度不计)进行裁剪可以得到一种梯形钢板零件,现有一边长为3(单位:米)的正三角形钢板(如图),沿平行于边![]() 的直线
的直线![]() 将
将![]() 剪去,得到所需的梯形钢材
剪去,得到所需的梯形钢材![]() ,记这个梯形钢板的周长为
,记这个梯形钢板的周长为![]() (单位:米),面积为
(单位:米),面积为![]() (单位:平方米).
(单位:平方米).
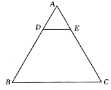
(1)求梯形![]() 的面积
的面积![]() 关于它的周长
关于它的周长![]() 的函数关系式;
的函数关系式;
(2)若在生产中,梯形![]() 的面积与周长之比(即
的面积与周长之比(即![]() )达到最大值时,零件才能符合使用要求,试确定这个梯形的周长
)达到最大值时,零件才能符合使用要求,试确定这个梯形的周长![]() 为多时,该零件才可以在生产中使用?
为多时,该零件才可以在生产中使用?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一艘轮船在航行中燃料费和它的速度的立方成正比.已知速度为每小时10千米时,燃料费是每小时6元,而其他与速度无关的费用是每小时96元,问轮船的速度是多少时,航行1千米所需的费用总和最少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在等腰梯形ABCD中,![]() ,
,![]() ,
,![]() ,E为AD中点,点O,F分别为BE,DE的中点,将
,E为AD中点,点O,F分别为BE,DE的中点,将![]() 沿BE折起到
沿BE折起到![]() 的位置,使得平面
的位置,使得平面![]() 平面BCDE(如图).
平面BCDE(如图).
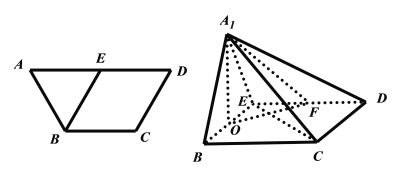
(1)求证:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)侧棱![]() 上是否存在点P,使得
上是否存在点P,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由
的值;若不存在,请说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com