
分析 (1)运用等差数列的通项公式,解方程可得首项为1,再由等差数列的通项公式即可得到所求;
(2)求得bn=2nan=(2n-1)•2n,再由数列的求和方法:错位相减法,结合等比数列的求和公式,化简整理即可得到所求.
解答 解:(1)依题意,由$\frac{1}{{a}_{1}{a}_{2}}$+$\frac{1}{{a}_{2}{a}_{3}}$=$\frac{2}{5}$,d=2,
可得$\frac{1}{{a}_{1}({a}_{1}+2)}$+$\frac{1}{({a}_{1}+2)({a}_{1}+4)}$=$\frac{2}{5}$,
解得a1=1(-5舍去),
即有an=a1+(n-1)d=1+2(n-1)=2n-1;
(2)bn=2nan=(2n-1)•2n,
前n项和Tn=1•2+3•22+5•23+…+(2n-1)•2n,
2Tn=1•22+3•23+5•24+…+(2n-1)•2n+1,
两式相减可得-Tn=2+23+24+…+2n+1-(2n-1)•2n+1
=2+$\frac{8(1-{2}^{n-1})}{1-2}$-(2n-1)•2n+1,
可得Tn=6+(2n-3)•2n+1.
点评 本题考查等差数列的通项公式的运用和求法,考查数列的求和方法:错位相减法,考查等比数列的求和公式的运用,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
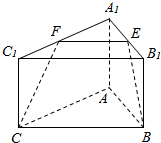 如图所示,三棱柱ABC-A1B1C1中,E,F分别是A1B1,A1C1的中点.截面BCFE将三棱柱分成两部分,你能说出多面体A1EF-ABC是什么样的几何体吗?多面体B1C1FE-BC是简单几何体还是组合体?为什么?
如图所示,三棱柱ABC-A1B1C1中,E,F分别是A1B1,A1C1的中点.截面BCFE将三棱柱分成两部分,你能说出多面体A1EF-ABC是什么样的几何体吗?多面体B1C1FE-BC是简单几何体还是组合体?为什么?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com