
【题目】已知点![]() 在抛物线
在抛物线![]()
![]() 上,
上, ![]() 点到抛物线
点到抛物线![]() 的焦点
的焦点![]() 的距离为2,直线
的距离为2,直线
![]()
![]() 与抛物线交于
与抛物线交于![]() 两点.
两点.
(1)求抛物线![]() 的方程;
的方程;
(2)若以![]() 为直径的圆与
为直径的圆与![]() 轴相切,求该圆的方程.
轴相切,求该圆的方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(Ⅰ)抛物线y2=2px(p>0)的准线为![]() ,由抛物线定义和已知条件可知
,由抛物线定义和已知条件可知![]() ,由此能求出抛物线方程.
,由此能求出抛物线方程.
(Ⅱ)联立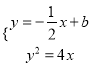 ,消x并化简整理得y2+8y-8b=0.依题意应有△=64+32b>0,解得b>-2.设A(x1,y1),B(x2,y2),则y1+y2=-8,y1y2=-8b,设圆心Q(x0,y0),则应有
,消x并化简整理得y2+8y-8b=0.依题意应有△=64+32b>0,解得b>-2.设A(x1,y1),B(x2,y2),则y1+y2=-8,y1y2=-8b,设圆心Q(x0,y0),则应有![]() ,因为以AB为直径的圆与x轴相切,得到圆半径为r=|y0|=4,由此能够推导出圆的方程.
,因为以AB为直径的圆与x轴相切,得到圆半径为r=|y0|=4,由此能够推导出圆的方程.
试题解析:
(1)抛物线![]()
![]() 的准线为
的准线为![]() ,
,
由抛物线定义和已知条件可知![]() ,
,
解得![]() ,故所求抛物线方程为
,故所求抛物线方程为![]() .
.
(2)联立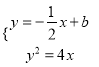 ,消
,消![]() 并化简整理得
并化简整理得![]() .
.
依题意应有![]() ,解得
,解得![]() .
.
设![]() ,则
,则![]() ,
,
设圆心![]() ,则应有
,则应有![]() .
.
因为以![]() 为直径的圆与
为直径的圆与![]() 轴相切,得到圆半径为
轴相切,得到圆半径为![]() ,
,
![]() .
.
所以![]() ,
,
解得![]() .
.
所以![]() ,所以圆心为
,所以圆心为![]() .
.
故所求圆的方程为![]() .
.


科目:高中数学 来源: 题型:
【题目】某设备的使用年数x与所支出的维修总费用y的统计数据如下表:
使用年数x(单位:年) | 2 | 3 | 4 | 5 | 6 |
维修费用y(单位:万元) | 1.5 | 4.5 | 5.5 | 6.5 | 7.0 |
根据上标可得回归直线方程为 ![]() =1.3x+
=1.3x+ ![]() ,若该设备维修总费用超过12万元,据此模型预测该设备最多可使用年.
,若该设备维修总费用超过12万元,据此模型预测该设备最多可使用年.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的方程为y=3+ ![]() .
.
(1)写出曲线C的一个参数方程;
(2)在曲线C上取一点P,过点P作x轴,y轴的垂线,垂足分别为A,B,求矩形OAPB的周长的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,AB⊥平面BB1C1C,∠BCC1= ![]() ,AB=BB1=2,BC=1,D为CC1中点.
,AB=BB1=2,BC=1,D为CC1中点. 
(1)求证:DB1⊥平面ABD;
(2)求二面角A﹣B1D﹣A1的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}为等差数列,公差为d,且0<d<1,a5≠ ![]() (k∈Z),sin2a3+2sina5cosa5=sin2a7 , 函数f(x)=dsin(wx+4d)(w>0)满足:在
(k∈Z),sin2a3+2sina5cosa5=sin2a7 , 函数f(x)=dsin(wx+4d)(w>0)满足:在 ![]() 上单调且存在
上单调且存在 ![]() ,则w范围是 .
,则w范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com