
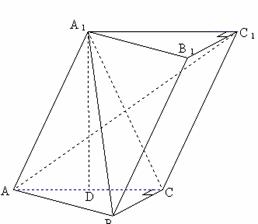
已知斜三棱柱![]() ,
,![]() ,
,![]() ,
,![]() 在底面
在底面![]() 上的射影恰为
上的射影恰为![]() 的中点
的中点![]() ,又知
,又知![]() 。
。
(I)求证:![]() 平面
平面![]() ;
;
(II)求![]() 到平面
到平面![]() 的距离;
的距离;
(III)求二面角![]() 的大小。
的大小。
|
解:(I)因为![]() 平面
平面![]() ,
,
 所以平面
所以平面![]() 平面
平面![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ,
,
得![]() ,又
,又![]()
所以![]() 平面
平面![]() ;
;
(II)因为![]() ,所以四边形
,所以四边形![]() 为
为
菱形,
故![]() ,又
,又![]() 为
为![]() 中点,知
中点,知![]() 。
。
取![]() 中点
中点![]() ,则
,则![]() 平面
平面![]() ,从而面
,从而面![]() 面
面![]() ,
,
过![]() 作
作![]() 于
于![]() ,则
,则![]() 面
面![]() ,
,
在![]() 中,
中,![]() ,故
,故![]() ,
,
即![]() 到平面
到平面![]() 的距离为
的距离为![]() 。
。
(III)过![]() 作
作![]() 于
于![]() ,连
,连![]() ,则
,则![]() ,
,
从而![]() 为二面角
为二面角![]() 的平面角,
的平面角,
在![]() 中,
中,![]() ,所以
,所以![]() ,
,
在![]() 中,
中,![]() ,
,
故二面角![]() 的大小为
的大小为![]() 。
。
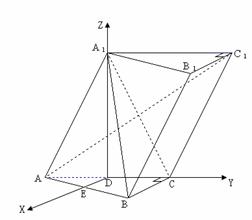
解法2:(I)如图,取![]() 的中点
的中点![]() ,则
,则![]() ,因为
,因为![]() ,
,
 所以
所以![]() ,又
,又![]() 平面
平面![]() ,
,
以![]() 为
为![]() 轴建立空间坐标系,
轴建立空间坐标系,
则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,由
,由![]() ,知
,知![]() ,
,
又![]() ,从而
,从而![]() 平面
平面![]() ;
;
(II)由![]()
![]() ,得
,得![]() 。
。
设平面![]() 的法向量为
的法向量为![]() ,
,![]() ,
,![]() ,所以
,所以
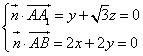 ,设
,设![]() ,则
,则![]()
所以点![]() 到平面
到平面![]() 的距离
的距离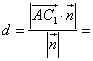
![]() 。
。
(III)再设平面![]() 的法向量为
的法向量为![]() ,
,![]() ,
,![]() ,
,
所以
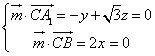 ,设
,设![]() ,则
,则![]() ,
,
故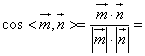
![]() ,根据法向量的方向,
,根据法向量的方向,
可知二面角![]() 的大小为
的大小为![]() 。
。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
(09年大丰调研)(10分)已知斜三棱柱![]() ,
,![]() ,
,![]() ,
,![]() 在底面
在底面![]() 上的射影恰为
上的射影恰为![]() 的中点
的中点![]() ,又知
,又知![]() 。
。
(I)求证:![]() 平面
平面![]() ;
;
(II)求![]() 到平面
到平面![]() 的距离;
的距离;
(III)求二面角![]() 余弦值的大小。
余弦值的大小。

查看答案和解析>>
科目:高中数学 来源: 题型:
(09年扬州中学2月月考)(10分)已知斜三棱柱![]() ,
,![]() ,
,![]() ,
,![]() 在底面
在底面![]() 上的射影恰为
上的射影恰为![]() 的中点
的中点![]() ,又知
,又知![]() 。
。
(I)求证:![]() 平面
平面![]() ;
;
(II)求![]() 到平面
到平面![]() 的距离;
的距离;
(III)求二面角![]() 余弦值的大小。
余弦值的大小。

查看答案和解析>>
科目:高中数学 来源:2011届重庆一中高三考前最后一次考试理数试卷 题型:解答题
(本小题满分12分)
已知斜三棱柱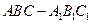 ,
,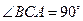 ,
, ,
,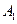 在底面
在底面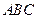 上的射影恰
上的射影恰
为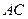 的中点
的中点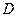 ,
,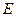 为
为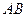 的中点,
的中点,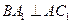 .
.
(I)求证: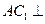 平面
平面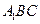 ;
;
(II)求二面角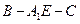 余弦值的大小.
余弦值的大小.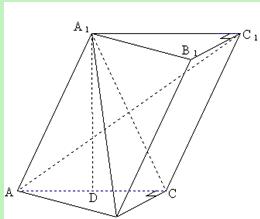
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省高三上学期10月月考数学试卷 题型:解答题
已知斜三棱柱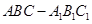 ,
,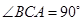 ,
,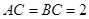 ,
,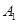 在底面
在底面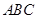 上的射影恰为
上的射影恰为 的中点
的中点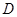 ,又知
,又知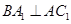 。
。
(I)求证: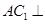 平面
平面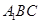 ;
;
(II)求二面角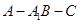 余弦值的大小。
余弦值的大小。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年重庆市高三最后一次模拟考试理数 题型:解答题
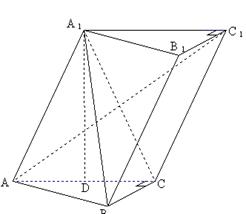
.(本小题满分12分)如图,已知斜三棱柱 ,
, ,
, ,
, 在底面
在底面 上的射影恰为
上的射影恰为 的中点
的中点 ,又知
,又知 .
.
(I)求证: ;
;
(II)求 到平面
到平面 的距离;
的距离;
(III)求二面角 .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com