
【题目】某公司要在一条笔直的道路边安装路灯,要求灯柱AB与底面垂直,灯杆BC与灯柱AB所在的平面与道路走向垂直,路灯C采用锥形灯罩,射出的管线与平面ABC部分截面如图中阴影所示,![]() 路宽AD=24米,设
路宽AD=24米,设![]()

(1)求灯柱AB的高h(用![]() 表示);
表示);
(2)此公司应该如何设置![]() 的值才能使制作路灯灯柱AB和灯杆BC所用材料的总长度最小?最小值为多少?
的值才能使制作路灯灯柱AB和灯杆BC所用材料的总长度最小?最小值为多少?
科目:高中数学 来源: 题型:
【题目】某理科考生参加自主招生面试,从7道题中(4道理科题3道文科题)不放回地依次任取3道作答.
(1)求该考生在第一次抽到理科题的条件下,第二次和第三次均抽到文科题的概率;
(2)规定理科考生需作答两道理科题和一道文科题,该考生答对理科题的概率均为![]() ,答对文科题的概率均为
,答对文科题的概率均为![]() ,若每题答对得10分,否则得零分.现该生已抽到三道题(两理一文),求其所得总分
,若每题答对得10分,否则得零分.现该生已抽到三道题(两理一文),求其所得总分![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在斜三棱柱![]() 中,底面
中,底面![]() 是边长为2的正三角形,侧棱长为
是边长为2的正三角形,侧棱长为![]() ,点
,点![]() 在底面
在底面![]() 的投影是线段
的投影是线段![]() 的中点
的中点![]() ,
,![]() 为侧棱
为侧棱![]() 的中点.
的中点.

(1)求证:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成二面角的正弦值.
所成二面角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 是过点
是过点![]() ,倾斜角为
,倾斜角为![]() 的直线,以直角坐标系
的直线,以直角坐标系![]() 的原点为极点,
的原点为极点, ![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(Ⅰ)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的一个参数方程;
的一个参数方程;
(Ⅱ)曲线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某自动包装机包袋的食盐中,随机抽取![]() 袋作为样本,按各袋的质量(单位:
袋作为样本,按各袋的质量(单位: ![]() )分成四组,
)分成四组, ![]() ,相应的样本频率分布直方图如图所示.
,相应的样本频率分布直方图如图所示.
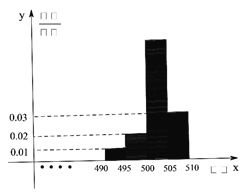
(Ⅰ)估计样本的中位数是多少?落入![]() 的频数是多少?
的频数是多少?
(Ⅱ)现从这台自动包装机包袋的大批量食盐中,随机抽取![]() 袋,记
袋,记![]() 表示食盐质量属于
表示食盐质量属于![]() 的袋数,依样本估计总体的统计思想,求
的袋数,依样本估计总体的统计思想,求![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 已知△ABC的三个内角A,B,C的对边分别为a,b,c,向量m=![]() ,n=
,n=![]() ,且m与n的夹角为
,且m与n的夹角为![]() .
.
(1)求角C;
(2)已知c=![]() ,S△ABC=
,S△ABC=![]() ,求a+b的值.
,求a+b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面四个命题:
①![]() 在定义域上单调递增;
在定义域上单调递增;
②若锐角![]() ,
,![]() 满足
满足![]() ,则
,则![]() ;
;
③![]() 是定义在
是定义在![]() 上的偶函数,且在
上的偶函数,且在![]() 上是增函数,若
上是增函数,若![]() ,则
,则![]() ;
;
④函数![]() 的一个对称中心是
的一个对称中心是![]() ;
;
其中真命题的序号为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 满足
满足![]() (
(![]() ),且
),且![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)若函数![]() 在区间
在区间![]() 上是单调函数,求实数
上是单调函数,求实数![]() 的取值范围;
的取值范围;
(3)若关于![]() 的方程
的方程![]() 有区间
有区间![]() 上有一个零点,求实数
上有一个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形CDEF为正方形,四边形ABCD为梯形,![]() ,
,![]() ,
,![]() ,
,![]() 平面ABCD.
平面ABCD.
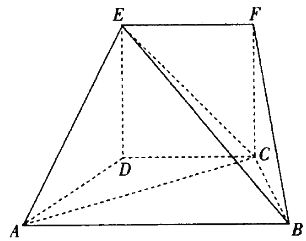
![]() 求BE与平面EAC所成角的正弦值;
求BE与平面EAC所成角的正弦值;
![]() 线段BE上是否存在点M,使平面
线段BE上是否存在点M,使平面![]() 平面DFM?若存在,求
平面DFM?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com