
【题目】已知抛物线![]() ,
,![]() 为其焦点,
为其焦点,![]() 为其准线,过
为其准线,过![]() 任作一条直线交抛物线于
任作一条直线交抛物线于![]() 两点,
两点,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 在
在![]() 上的射影,
上的射影,![]() 为
为![]() 的中点,给出下列命题:
的中点,给出下列命题:
(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;
;
(4)![]() 与
与![]() 的交点的
的交点的![]() 轴上;(5)
轴上;(5)![]() 与
与![]() 交于原点.
交于原点.
其中真命题的序号为_________.
【答案】(1)(2)(3)(4)(5)
【解析】
(1)由![]() 、
、![]() 在抛物线上,根据抛物线的定义可知
在抛物线上,根据抛物线的定义可知![]() ,
,![]() ,从而有相等的角,由此可判断
,从而有相等的角,由此可判断![]() ;
;
(2)取![]() 的中点
的中点![]() ,利用中位线即抛物线的定义可得
,利用中位线即抛物线的定义可得![]() ,从而可得
,从而可得![]() ;
;
(3)由(2)知,![]() 平分
平分![]() ,从而可得
,从而可得![]() ,根据
,根据![]() ,利用垂直于同一直线的两条直线平行,可得结论;
,利用垂直于同一直线的两条直线平行,可得结论;
(4)取![]() 与
与![]() 轴的交点
轴的交点![]() ,可得
,可得![]() ,可得出
,可得出![]() 的中点在
的中点在![]() 轴上,从而得出结论;
轴上,从而得出结论;
(5)设直线![]() 的方程为
的方程为![]() ,设点
,设点![]() 、
、![]() ,证明出
,证明出![]() 、
、![]() 、
、![]() 三点共线,同理得出
三点共线,同理得出![]() 、
、![]() 、
、![]() 三点共线,由此可得出结论.
三点共线,由此可得出结论.
(1)由于![]() 、
、![]() 在抛物线上,且
在抛物线上,且![]() 、
、![]() 分别为
分别为![]() 、
、![]() 在准线
在准线![]() 上的射影,
上的射影,
根据抛物线的定义可知![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,![]() ,则
,则![]() ,
,
即![]() ,
,![]() ,则
,则![]() ,即
,即![]() ,(1)正确;
,(1)正确;

(2)取![]() 的中点
的中点![]() ,则
,则![]() ,
,![]() ,即
,即![]() ,
,
(2)正确;

(3)由(2)知,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() 平分
平分![]() ,
,![]() ,由于
,由于![]() ,
,![]() ,(3)正确;
,(3)正确;
(4)取![]() 与
与![]() 轴的交点
轴的交点![]() ,则
,则![]() ,
,![]() 轴,可知
轴,可知![]() ,
,
![]() ,即点
,即点![]() 为
为![]() 的中点,由(3)知,
的中点,由(3)知,![]() 平分
平分![]() ,
,![]() 过点
过点![]() ,
,
所以,![]() 与
与![]() 的交点的
的交点的![]() 轴上,(4)正确;
轴上,(4)正确;
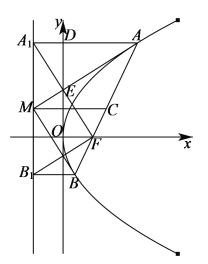
(5)设直线![]() 的方程为
的方程为![]() ,设点
,设点![]() 、
、![]() ,则点
,则点![]() 、
、![]() ,
,
将直线![]() 的方程与抛物线的方程联立,消去
的方程与抛物线的方程联立,消去![]() 得,
得,![]() ,
,
由韦达定理得![]() ,
,![]() ,
,
直线![]() 的斜率为
的斜率为 ,
,
直线![]() 的斜率为
的斜率为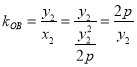 ,
,![]() ,
,
则![]() 、
、![]() 、
、![]() 三点共线,同理得出
三点共线,同理得出![]() 、
、![]() 、
、![]() 三点共线,
三点共线,
所以,![]() 与
与![]() 交于原点,(5)正确.
交于原点,(5)正确.
综上所述,真命题的序号为:(1)(2)(3)(4)(5).
故答案为:(1)(2)(3)(4)(5).


科目:高中数学 来源: 题型:
【题目】如图,已知曲线![]() ,曲线
,曲线![]() ,P是平面上一点,若存在过点P的直线与
,P是平面上一点,若存在过点P的直线与![]() 都有公共点,则称P为“C1—C2型点”.
都有公共点,则称P为“C1—C2型点”.
(1)在正确证明![]() 的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
(2)设直线![]() 与
与![]() 有公共点,求证
有公共点,求证![]() ,进而证明原点不是“C1—C2型点”;
,进而证明原点不是“C1—C2型点”;
(3)求证:圆![]() 内的点都不是“C1—C2型点”.
内的点都不是“C1—C2型点”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S-ABCD中,底面ABCD是菱形,![]() ,
,![]() 为等边三角形,G是线段SB上的一点,且SD//平面GAC.
为等边三角形,G是线段SB上的一点,且SD//平面GAC.
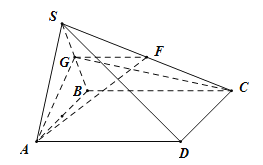
(1)求证:G为SB的中点;
(2)若F为SC的中点,连接GA,GC,FA,FG,平面SAB⊥平面ABCD,![]() ,求三棱锥F-AGC的体积.
,求三棱锥F-AGC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】辊子是客家传统农具,南方农民犁开田地后,仍有大的土块.农人便用六片叶齿组成辊轴,两侧装上木板,人跨开两脚站立,既能掌握平衡,又能增加重量,让牛拉动辊轴前进,压碎土块,以利于耕种.这六片叶齿又对应着菩萨六度,即布施持戒忍辱精进禅定与般若.若甲乙每人依次有放回地从这六片叶齿中随机取一片,则这两人选的叶齿对应的“度”相同的概率为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若点![]() 在直线
在直线![]() 上,且
上,且![]() ,求直线
,求直线![]() 的斜率;
的斜率;
(2)若![]() ,求曲线
,求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 将
将![]() 的图象上所有点向左平移
的图象上所有点向左平移![]() 个单位,然后纵坐标不变,横坐标缩短为原来的
个单位,然后纵坐标不变,横坐标缩短为原来的![]() ,得到函数
,得到函数![]() 的图象.若
的图象.若![]() 为偶函数,且最小正周期为
为偶函数,且最小正周期为![]() ,则( )
,则( )
A.![]() 图象与
图象与![]() 对称B.
对称B.![]() 在
在![]() 单调递增
单调递增
C.![]() 在
在![]() 有且仅有3个解D.
有且仅有3个解D.![]() 在
在![]() 有仅有3个极大值点
有仅有3个极大值点
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com