
【题目】如图,三棱柱ABC﹣A1B1C1中,侧面BB1C1C为菱形,AB⊥B1C.
(Ⅰ)证明:A1C1=AB1;
(Ⅱ)若AC⊥AB1 , ∠BCC1=120°,AB=BC,求二面角A﹣A1B1﹣C1的余弦值.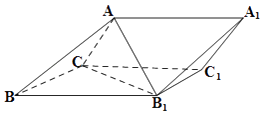
【答案】(Ⅰ)证明:连接BC1 , 交B1C于点O,连接AO,∵侧面BB1C1C为菱形,∴B1C⊥BC1 , 且O为B1C及BC1的中点.
又AB⊥B1C,∴B1C⊥平面ABO.故B1C⊥AO.又B1O=CO,
故AC=AB1 .
又AC=A1C1 , ∴A1C1=AB1;
(Ⅱ)解:∵AC⊥AB1 , 且O为B1C的中点,∴AO=CO.
又∵AB=BC,∴△BOA≌△BOC.故OA⊥OB,从而OA,OB,OB1两两垂直.以O为坐标原点,OB的方向为x轴正方向,设|OB|=1,建立如图所示的空间直角坐标系O﹣xyz.
∵∠BCC1=120°,∴∠CBB1=60°,∴△CBB1为等边三角形,又AB=BC,
则  ,B(1,0,0),
,B(1,0,0), 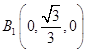 ,
,  .
.
设 ![]() 是平面AA1B1的法向量,则
是平面AA1B1的法向量,则  ,
,
∴可取 ![]() .
.
设 ![]() 是平面A1B1C1的法向量,则同理可取
是平面A1B1C1的法向量,则同理可取 ![]() .
.
则 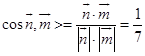 .
.
∴结合图形知二面角A﹣A1B1﹣C的余弦值为 ![]() .
.
【解析】(Ⅰ)连结BC1 , 交B1C于点O,连结AO,可证B1C⊥平面ABO,可得B1C⊥AO,B1O=CO,进而可得A1C1=AB1;(Ⅱ)以O为坐标原点, ![]() 的方向为x轴的正方向,|
的方向为x轴的正方向,| ![]() |为单位长度,
|为单位长度, ![]() 的方向为y轴的正方向,
的方向为y轴的正方向, ![]() 的方向为z轴的正方向建立空间直角坐标系,分别可得两平面的法向量,可得所求余弦值.
的方向为z轴的正方向建立空间直角坐标系,分别可得两平面的法向量,可得所求余弦值.


科目:高中数学 来源: 题型:
【题目】某厂生产产品x件的总成本c(x)=1200+![]() x3(万元),已知产品单价P(万元)与产品件数x满足:p2=
x3(万元),已知产品单价P(万元)与产品件数x满足:p2=![]() ,生产100件这样的产品单价为50万元.
,生产100件这样的产品单价为50万元.
(1)设产量为x件时,总利润为L(x)(万元),求L(x)的解析式;
(2)产量x定为多少件时总利润L(x)(万元)最大?并求最大值(精确到1万元).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 设an是Sn与2的等差中项,数列{bn}中,b1=1,点P(bn , bn+1)在直线y=x+2上.
(Ⅰ)求an , bn;
(Ⅱ)若数列{bn}的前n项和为Bn , 比较 ![]() +
+ ![]() +…+
+…+ ![]() 与1的大小.
与1的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 及点
及点![]() ,
, ![]() .
.
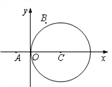
(1)若直线![]() 平行于
平行于![]() ,与圆
,与圆![]() 相交于
相交于![]() ,
, ![]() 两点,
两点, ![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)在圆C上是否存在点P,使得![]() ?若存在,求点P的个数;若不存在,说明理由.
?若存在,求点P的个数;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn=n2 , {bn}为等比数列,且a1=b1 , b2(a2﹣a1)=b1 .
(1)求数列{an},{bn}的通项公式.
(2)设cn=anbn , 求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
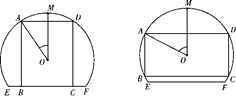
【题目】如图,一块弓形余布料EMF,点M为弧![]() 的中点,其所在圆O的半径为4 dm(圆心O在弓形EMF内),∠EOF=
的中点,其所在圆O的半径为4 dm(圆心O在弓形EMF内),∠EOF=![]() .将弓形余布料裁剪成尽可能大的矩形ABCD(不计损耗), AD∥EF,且点A、D在弧
.将弓形余布料裁剪成尽可能大的矩形ABCD(不计损耗), AD∥EF,且点A、D在弧![]() 上,设∠AOD=
上,设∠AOD=![]() .
.
(1)求矩形ABCD的面积S关于![]() 的函数关系式;
的函数关系式;
(2)当矩形ABCD的面积最大时,求cos![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC为等腰直角三角形,AC=BC=4,∠ACB=90°,D、E分别是边AC和AB的中点,现将△ADE沿DE折起,使面ADE⊥面DEBC,H、F分别是边AD和BE的中点,平面BCH与AE、AF分别交于I、G两点
(Ⅰ)求证:IH∥BC;
(Ⅱ)求直线AE与平面角GIC所成角的正弦值.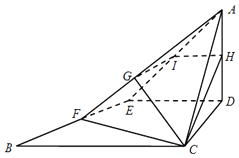
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p:关于x的不等式|x﹣2|+|x+2|>m的解集是R; q:关于x的不等式x2+mx+4>0的解集是R.则p成立是q成立的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.即不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com