
【题目】如图,四棱锥P-ABCD中,底面ABCD为矩形,PD⊥平面ABCD,点E、F分别是AB和PC的中点.
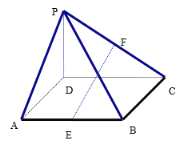
(1)求证:AB⊥平面PAD;
(2)求证:EF//平面PAD.
【答案】(1)证明见解析(2)证明见解析
【解析】
(1)证明PA⊥AB,AD⊥AB,证得AB⊥平面PAD.
(2)取CD的中点G,由FG是三角形CPD的中位线,可得 FG∥PD,再由矩形的性质得 EG∥AD,证明平面EFG∥平面PAD,从而证得EF∥平面PAD.
(1)∵侧棱PA垂直于底面,∴PA⊥AB.又底面ABCD是矩形,∴AD⊥AB,
这样,AB垂直于平面PAD内的两条相交直线,∴AB⊥平面PAD.
(2)取CD的中点G,∵E、F分别是AB、PC的中点,∴FG是三角形CPD的中位线,
∴FG∥PD,FG∥面PAD.∵底面ABCD是矩形,∴EG∥AD,EG∥平面PAD.
故平面EFG∥平面PAD,∴EF∥平面PAD.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设an= ![]() sin
sin ![]() ,Sn=a1+a2+…+an , 在S1 , S2 , …S100中,正数的个数是( )
,Sn=a1+a2+…+an , 在S1 , S2 , …S100中,正数的个数是( )
A.25
B.50
C.75
D.100
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着共享单车的蓬勃发展,越来越多的人将共享单车作为短距离出行的交通工具.为了解不同年龄的人们骑乘单车的情况,某共享单车公司对某区域不同年龄的骑乘者进行了调查,得到数据如下:
年龄 | 15 | 25 | 35 | 45 | 55 | 65 |
骑乘人数 | 95 | 80 | 65 | 40 | 35 | 15 |
(1)求![]() 关于
关于![]() 的线性回归方程,并估计年龄为40岁人群的骑乘人数;
的线性回归方程,并估计年龄为40岁人群的骑乘人数;
(2)为了回馈广大骑乘者,该公司在五一当天通过![]() 向每位骑乘者的前两次骑乘分别随机派送一张面额为1元,或2元,或3元的骑行券.已知骑行一次获得1元券,2元券,3元券的概率分别是
向每位骑乘者的前两次骑乘分别随机派送一张面额为1元,或2元,或3元的骑行券.已知骑行一次获得1元券,2元券,3元券的概率分别是![]() ,
,![]() ,
,![]() ,且每次获得骑行券的面额相互独立.若一名骑乘者五一当天使用了两次该公司的共享单车,记该骑乘者当天获得的骑行券面额之和为
,且每次获得骑行券的面额相互独立.若一名骑乘者五一当天使用了两次该公司的共享单车,记该骑乘者当天获得的骑行券面额之和为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式:
 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校选派甲、乙、丙、丁、戊5名学生代表学校参加市级“演讲”和“诗词”比赛,下面是他们的一段对话.甲说:“乙参加‘演讲’比赛”;乙说:“丙参加‘诗词’比赛”;丙说“丁参加‘演讲’比赛”;丁说:“戊参加‘诗词’比赛”;戊说:“丁参加‘诗词’比赛”.
已知这5个人中有2人参加“演讲”比赛,有3人参加“诗词”比赛,其中有2人说的不正确,且参加“演讲”的2人中只有1人说的不正确.根据以上信息,可以确定参加“演讲”比赛的学生是
A. 甲和乙 B. 乙和丙 C. 丁和戊 D. 甲和丁
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知无穷数列![]() ,
,![]() 是公差分别为
是公差分别为![]() 、
、![]() 的等差数列,记
的等差数列,记![]() (
(![]() ),其中
),其中![]() 表示不超过
表示不超过![]() 的最大整数,即
的最大整数,即![]() .
.
(1)直接写出数列![]() ,
,![]() 的前4项,使得数列
的前4项,使得数列![]() 的前4项为:2,3,4,5;
的前4项为:2,3,4,5;
(2)若![]() ,求数列
,求数列![]() 的前
的前![]() 项的和
项的和![]() ;
;
(3)求证:数列![]() 为等差数列的必要非充分条件是
为等差数列的必要非充分条件是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】运动员参加射击比赛,每人射击4次(每次射一发),比赛规定:全不中得0分,只中一弹得15分,中两弹得40分,中三弹得65分,中四弹得100分.已知某一运动员每一次射击的命中率为![]() ,则他的得分期望为_____.
,则他的得分期望为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com