
【题目】给出集合![]()
(1)若![]() 求证:函数
求证:函数![]()
(2)由(1)可知,![]() 是周期函数且是奇函数,于是张三同学得出两个命题:
是周期函数且是奇函数,于是张三同学得出两个命题:
命题甲:集合M中的元素都是周期函数;命题乙:集合M中的元素都是奇函数,请对此给出判断,如果正确,请证明;如果不正确,请举出反例;
(3)设![]() 为常数,且
为常数,且![]() 求
求![]() 的充要条件并给出证明.
的充要条件并给出证明.
【答案】(1)证明见解析;(2)命题甲正确,命题乙不正确;(3)![]() 的充要条件为
的充要条件为![]() ,
,![]() ,且
,且![]() .证明见解析.
.证明见解析.
【解析】
(1)![]() 转化证明
转化证明![]() 等价于
等价于![]() ,利用两角和与差的三角函数化简求解即可.(2)命题甲正确.集合
,利用两角和与差的三角函数化简求解即可.(2)命题甲正确.集合![]() 中的元素都是周期为6的周期函数,验证
中的元素都是周期为6的周期函数,验证![]() 即可,命题乙不正确.集合
即可,命题乙不正确.集合![]() 中的元素不都是奇函数,列举反例即可;(3)由函数的周期性,结合正弦公式,化简可得所求
中的元素不都是奇函数,列举反例即可;(3)由函数的周期性,结合正弦公式,化简可得所求![]() 的值.
的值.
(1)证明:![]() 转化证明
转化证明![]()
![]() ,
,
左边![]()
![]() 右边;
右边;
(2)命题甲正确.集合![]() 中的元素都是周期为6的周期函数.
中的元素都是周期为6的周期函数.
![]() ,可得
,可得![]() ,
,
即有![]() ,可得
,可得![]() ,
,
即![]() ,
,![]() 为最小正周期为6的函数;
为最小正周期为6的函数;
命题乙不正确.集合![]() 中的元素不都是奇函数.
中的元素不都是奇函数.
如![]() 是奇函数;
是奇函数;![]() 不是奇函数.
不是奇函数.
(3)由![]() ,可得
,可得![]() ,
,
即有![]() ,可得
,可得![]() ,
,
即![]() ,
,
![]() ,可得
,可得![]() ,
,
即为![]() ,
,
即为![]() ,可得
,可得![]() ,
,![]() ,且
,且![]() ,
,
可得![]() ,
,![]() ,且
,且![]() .
.
则![]() 的充要条件为
的充要条件为![]() ,
,![]() ,且
,且![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】为研究某种图书每册的成本费![]() (元)与印刷数
(元)与印刷数![]() (千册)的关系,收集了一些数据并作了初步处理,得到了下面的散点图及一些统计量的值.
(千册)的关系,收集了一些数据并作了初步处理,得到了下面的散点图及一些统计量的值.

|
|
|
|
|
|
|
15.25 | 3.63 | 0.269 | 2085.5 |
| 0.787 | 7.049 |
表中![]() ,
, ![]() .
.
(1)根据散点图判断: ![]() 与
与![]() 哪一个更适宜作为每册成本费
哪一个更适宜作为每册成本费![]() (元)与印刷数
(元)与印刷数![]() (千册)的回归方程类型?(只要求给出判断,不必说明理由)
(千册)的回归方程类型?(只要求给出判断,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程(回归系数的结果精确到0.01);
的回归方程(回归系数的结果精确到0.01);
(3)若每册书定价为10元,则至少应该印刷多少册才能使销售利润不低于78840元?(假设能够全部售出,结果精确到1)
(附:对于一组数据![]() ,
, ![]() ,…,
,…, ![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥![]() ﹣
﹣![]() 中,底面ABCD是矩形,
中,底面ABCD是矩形,![]() ⊥平面
⊥平面![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是线段
是线段![]() 上的点.
上的点.
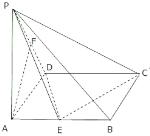
(1)当![]() 是
是![]() 的中点时,求证:
的中点时,求证:![]() ∥平面
∥平面![]() .
.
(2)当![]() :
:![]() = 2:1时,求二面角
= 2:1时,求二面角![]() ﹣
﹣![]() ﹣
﹣![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学生在开学季准备销售一种文具盒进行试创业,在一个开学季内,每售出1盒该产品获利润30元,未售出的产品,每盒亏损10元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了160盒该产品,以![]() (单位:盒,
(单位:盒, ![]() )表示这个开学季内的市场需求量,
)表示这个开学季内的市场需求量, ![]() (单位:元)表示这个开学季内经销该产品的利润.
(单位:元)表示这个开学季内经销该产品的利润.
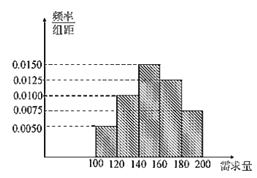
(1)根据直方图估计这个开学季内市场需求量![]() 的平均数;
的平均数;
(2)将![]() 表示为
表示为![]() 的函数;
的函数;
(3)根据直方图估计利润![]() 不少于4000元的概率.
不少于4000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 分别为左,右焦点,
分别为左,右焦点,![]() 分别为左,右顶点,D为上顶点,原点
分别为左,右顶点,D为上顶点,原点![]() 到直线
到直线![]() 的距离为
的距离为![]() .设点
.设点![]() 在第一象限,纵坐标为t,且
在第一象限,纵坐标为t,且![]() 轴,连接
轴,连接![]() 交椭圆于点
交椭圆于点![]() .
.
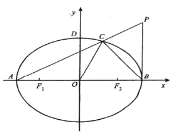
(1)求椭圆![]() 的方程;
的方程;
(2)(文)若三角形![]() 的面积等于四边形
的面积等于四边形![]() 的面积,求直线
的面积,求直线![]() 的方程;
的方程;
(理)求过点![]() 的圆方程(结果用t表示)
的圆方程(结果用t表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
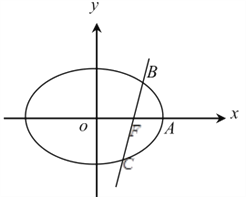
【题目】【2018届四川省成都市第七中学高三上学期模拟】已知椭圆![]() 的一个焦点
的一个焦点![]() ,且过点
,且过点![]() ,右顶点为
,右顶点为![]() ,经过点
,经过点![]() 的动直线
的动直线![]() 与椭圆交于
与椭圆交于![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)![]() 是椭圆
是椭圆![]() 上一点,
上一点, ![]() 的角平分线交
的角平分线交![]() 轴于
轴于![]() ,求
,求![]() 的长;
的长;
(3)在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得点
,使得点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 落在
落在![]() 上?若存在,求出
上?若存在,求出![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知椭圆两个焦点的坐标分别是(-2,0),(2,0),并且经过点![]() ,求它的标准方程;
,求它的标准方程;
(2)已知双曲线两个焦点的坐标分别是(0,-6),(0,6),并且经过点(2,-5),求它的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() (
(![]() ),满足
),满足![]() ,且
,且![]() 在
在![]() 时恒成立.
时恒成立.
(1)求![]() 、
、![]() 的值;
的值;
(2)若![]() ,解不等式
,解不等式![]() ;
;
(3)是否存在实数![]() ,使函数
,使函数![]() 在区间
在区间![]() 上有最小值
上有最小值![]() ?若存在,请求出
?若存在,请求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com