
ЁОЬтФПЁПЙигкКЏЪ§fЃЈxЃЉ![]() ЃЈxЁЪRЃЉЃЌгаЯТЪіЫФИіНсТлЃК
ЃЈxЁЪRЃЉЃЌгаЯТЪіЫФИіНсТлЃК
ЂйШЮвтxЁЪRЃЌЕШЪНfЃЈЉxЃЉ+fЃЈxЃЉЃН0КуГЩСЂЃЛ
ЂкШЮвтx1ЃЌx2ЁЪRЃЌШєx1Ёйx2ЃЌдђвЛЖЈгаfЃЈx1ЃЉЁйfЃЈx2ЃЉЃЛ
ЂлДцдкmЁЪЃЈ0ЃЌ1ЃЉЃЌЪЙЕУЗНГЬ|fЃЈxЃЉ|ЃНmгаСНИіВЛЕШЪЕЪ§ИљЃЛ
ЂмДцдкkЁЪЃЈ1ЃЌ+ЁоЃЉЃЌЪЙЕУКЏЪ§gЃЈxЃЉЃНfЃЈxЃЉЉkxдкRЩЯгаШ§ИіСуЕуЃЎ
ЦфжаАќКЌСЫЫљгае§ШЗНсТлБрКХЕФбЁЯюЮЊЃЈ ЃЉ
A.ЂйЂкЂлЂмB.ЂйЂкЂлC.ЂйЂкЂмD.ЂйЂк
ЁОД№АИЁПB
ЁОНтЮіЁП
ИљОнКЏЪ§ЕФЦцХМадХаЖЯЂйЕФе§ШЗадЃЌИљОнКЏЪ§ЕФЕЅЕїадХаЖЯЂкЕФе§ШЗадЃЌИљОн![]() ЕФЭМЯёХаЖЯЂлЕФе§ШЗадЃЌИљОн
ЕФЭМЯёХаЖЯЂлЕФе§ШЗадЃЌИљОн![]() гы
гы![]() ЕФЭМЯёХаЖЯЂмЕФе§ШЗад.
ЕФЭМЯёХаЖЯЂмЕФе§ШЗад.
КЏЪ§![]() ЕФЖЈвхгђЮЊ
ЕФЖЈвхгђЮЊ![]() ЃЌЧв
ЃЌЧв![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЌМДКЏЪ§ЮЊЦцКЏЪ§ЃЌЙЪЂйе§ШЗ.
ЃЌМДКЏЪ§ЮЊЦцКЏЪ§ЃЌЙЪЂйе§ШЗ.
![]() ЮЊ
ЮЊ![]() ЩЯЕФЦцКЏЪ§ЃЌ
ЩЯЕФЦцКЏЪ§ЃЌ![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЮЊдіКЏЪ§ЃЌЫљвд
ЮЊдіКЏЪ§ЃЌЫљвд![]() дк
дк![]() ЩЯЪЧдіКЏЪ§ЃЌЫљвдЂке§ШЗ.
ЩЯЪЧдіКЏЪ§ЃЌЫљвдЂке§ШЗ.
![]() ЪЧ
ЪЧ![]() ЩЯЕФЦцКЏЪ§ЁЂдіКЏЪ§ЃЌЧвЕБ
ЩЯЕФЦцКЏЪ§ЁЂдіКЏЪ§ЃЌЧвЕБ![]() ЪБЃЌ
ЪБЃЌ![]() .дђ
.дђ![]() ЮЊХМКЏЪ§ЃЌЧвЕБ
ЮЊХМКЏЪ§ЃЌЧвЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ![]() ЕндіЃЛЕБ
ЕндіЃЛЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛЕБ
ЃЛЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЕнМѕ.гЩДЫЛГі
ЕнМѕ.гЩДЫЛГі![]() ЕФЭМЯёШчЯТЭМЫљЪОЃЌгЩЭМПЩжЊЃЌЕБ
ЕФЭМЯёШчЯТЭМЫљЪОЃЌгЩЭМПЩжЊЃЌЕБ![]() ЪЧЃЌ
ЪЧЃЌ![]() гы
гы![]() гаСНИіВЛЭЌЕФНЛЕуЃЌЫљвдЂле§ШЗ.
гаСНИіВЛЭЌЕФНЛЕуЃЌЫљвдЂле§ШЗ.
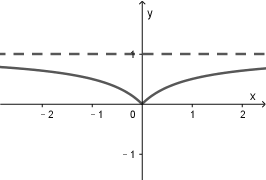
ЛГі![]() гы
гы![]() ЕФЭМЯёШчЯТЭМЫљЪОЃЌгЩЭМПЩжЊЃЌЕБ
ЕФЭМЯёШчЯТЭМЫљЪОЃЌгЩЭМПЩжЊЃЌЕБ![]() ЪБЃЌСНИіКЏЪ§ЭМЯёУЛгаШ§ИіНЛЕуЃЌЫљвдЂме§ШЗ.жЄУїШчЯТЃКЕБ
ЪБЃЌСНИіКЏЪ§ЭМЯёУЛгаШ§ИіНЛЕуЃЌЫљвдЂме§ШЗ.жЄУїШчЯТЃКЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЫљвд
ЃЌЫљвд![]() гк
гк![]() ЕФЭМЯёЯрЧа.ЕБ
ЕФЭМЯёЯрЧа.ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЫљвд
ЃЌЫљвд![]() гк
гк![]() ЕФЭМЯёЯрЧа.НсКЯЭМЯёПЩжЊ
ЕФЭМЯёЯрЧа.НсКЯЭМЯёПЩжЊ![]() гы
гы![]() ЕФЭМЯёжЛгавЛИіЙЋЙВЕуЃЌЕБ
ЕФЭМЯёжЛгавЛИіЙЋЙВЕуЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() гы
гы![]() ЕФЭМЯёвВжЛгавЛИіЙЋЙВЕу.
ЕФЭМЯёвВжЛгавЛИіЙЋЙВЕу.
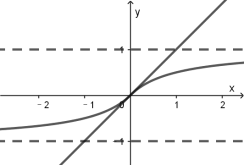
ЙЪбЁЃКB



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯжгавЛЖЮГЄЖШЮЊ![]() ЕФФОЙїЃЌЯЃЭћНЋЦфОтГЩОЁПЩФмЖрЕФаЁЖЮЃЌвЊЧѓУПвЛаЁЖЮЕФГЄЖШЖМЪЧећЪ§ЃЌВЂЧвШЮКЮвЛИіЪБПЬЃЌЕБЧАзюГЄЕФвЛЖЮЖМбЯИёаЁгкЕБЧАзюЖЬЕФвЛЖЮГЄЖШЕФ2БЖЃЌМЧЖд
ЕФФОЙїЃЌЯЃЭћНЋЦфОтГЩОЁПЩФмЖрЕФаЁЖЮЃЌвЊЧѓУПвЛаЁЖЮЕФГЄЖШЖМЪЧећЪ§ЃЌВЂЧвШЮКЮвЛИіЪБПЬЃЌЕБЧАзюГЄЕФвЛЖЮЖМбЯИёаЁгкЕБЧАзюЖЬЕФвЛЖЮГЄЖШЕФ2БЖЃЌМЧЖд![]() ЗћКЯЬѕМўЪБЕФзюЖраЁЖЮЪ§ЮЊ
ЗћКЯЬѕМўЪБЕФзюЖраЁЖЮЪ§ЮЊ![]() ЃЌдђЃЈ ЃЉЁЃ
ЃЌдђЃЈ ЃЉЁЃ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
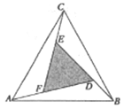
ЁОЬтФПЁПедЫЌЪЧЮвЙњЙХДњЪ§бЇМвЁЂЬьЮФбЇМвЃЌДѓдМдкЙЋдЊ222ФъЃЌедЫЌЮЊЁЖжмїТЫуОЁЗвЛЪщзїађЪБЃЌНщЩмСЫЁАЙДЙЩдВЗНЭМЁБЃЌврГЦЁАедЫЌьХЭМЁБЃЈвдЯвЮЊБпГЄЕУЕНЕФе§ЗНаЮзщГЩЃЉ.РрБШЁАедЫЌЯвЭМЁБЃЌПЩРрЫЦЕиЙЙдьШчЯТЭМЫљЪОЕФЭМаЮЃЌЫќЪЧгЩ3ИіШЋЕШЕФШ§НЧаЮгыжаМфЕФвЛИіаЁЕШБпШ§НЧаЮЦДГЩЕФвЛИіДѓЕШБпШ§НЧаЮЃЌЩш![]() ЃЌШєдкДѓЕШБпШ§НЧаЮжаЫцЛњШЁвЛЕуЃЌдђДЫЕуШЁздаЁЕШБпШ§НЧаЮЕФИХТЪЪЧ__________ЃЎ
ЃЌШєдкДѓЕШБпШ§НЧаЮжаЫцЛњШЁвЛЕуЃЌдђДЫЕуШЁздаЁЕШБпШ§НЧаЮЕФИХТЪЪЧ__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП2018Фъ8дТ8ШеЪЧЮвЙњЕкЪЎИіШЋУёНЁЩэШеЃЌЦфжїЬтЪЧЃКаТЪБДњШЋУёНЁЩэЖЏЦ№РДЁЃФГЪаЮЊСЫНтШЋУёНЁЩэЧщПіЃЌЫцЛњДгФГаЁЧјОгУёжаГщШЁСЫ40ШЫЃЌНЋЫћУЧЕФФъСфЗжГЩ7ЖЮЃК[10ЃЌ20ЃЉЃЌ[20ЃЌ30ЃЉЃЌ[30ЃЌ40ЃЉЃЌ[40ЃЌ50ЃЉЃЌ[50ЃЌ60ЃЉЃЌ[60ЃЌ70ЃЉЃЌ[70ЃЌ80]КѓЕУЕНШчЭМЫљЪОЕФЦЕТЪЗжВМжБЗНЭМЁЃ

ЃЈ1ЃЉЪдЧѓет40ШЫФъСфЕФЦНОљЪ§ЁЂжаЮЛЪ§ЕФЙРМЦжЕЃЛ
ЃЈ2ЃЉЃЈiЃЉШєДгбљБОжаФъСфдк[50ЃЌ70ЃЉЕФОгУёжаШЮШЁ2ШЫдљЫЭНЁЩэПЈЃЌЧѓет2ШЫжажСЩйга1ШЫФъСфВЛЕЭгк60ЫъЕФИХТЪЃЛ
ЃЈЂЂЃЉвбжЊИУаЁЧјФъСфдк[10ЃЌ80]ФкЕФзмШЫЪ§ЮЊ2000ЃЌШє18ЫъвдЩЯЃЈКЌ18ЫъЃЉЮЊГЩФъШЫЃЌЪдЙРМЦИУаЁЧјФъСфВЛГЌЙ§80ЫъЕФГЩФъШЫШЫЪ§ЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкжБНЧзјБъЯЕ![]() жаЃЌЧњЯп
жаЃЌЧњЯп![]() ЕФВЮЪ§ЗНГЬЮЊ
ЕФВЮЪ§ЗНГЬЮЊ![]() ЃЈ
ЃЈ![]() ЮЊВЮЪ§ЃЉЃЎMЪЧЧњЯп
ЮЊВЮЪ§ЃЉЃЎMЪЧЧњЯп![]() ЩЯЕФЖЏЕуЃЌНЋЯпЖЮOMШЦOЕуЫГЪБеыа§зЊ
ЩЯЕФЖЏЕуЃЌНЋЯпЖЮOMШЦOЕуЫГЪБеыа§зЊ![]() ЕУЕНЯпЖЮONЃЌЩшЕуNЕФЙьМЃЮЊЧњЯп
ЕУЕНЯпЖЮONЃЌЩшЕуNЕФЙьМЃЮЊЧњЯп![]() ЃЎвдзјБъдЕуOЮЊМЋЕуЃЌ
ЃЎвдзјБъдЕуOЮЊМЋЕуЃЌ![]() жсе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЎ
жсе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЎ
ЃЈ1ЃЉЧѓЧњЯп![]() ЕФМЋзјБъЗНГЬЃЛ
ЕФМЋзјБъЗНГЬЃЛ
ЃЈ2ЃЉдкЃЈ1ЃЉЕФЬѕМўЯТЃЌШєЩфЯп![]() гыЧњЯп
гыЧњЯп![]() ЗжБ№НЛгкA, BСНЕуЃЈГ§МЋЕуЭтЃЉЃЌЧвгаЖЈЕу
ЗжБ№НЛгкA, BСНЕуЃЈГ§МЋЕуЭтЃЉЃЌЧвгаЖЈЕу![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФУцЛ§ЃЎ
ЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПКЏЪ§fЃЈxЃЉЃНlog2ЃЈkx2+4kx+3ЃЉЃЎЂйШєfЃЈxЃЉЕФЖЈвхгђЮЊRЃЌдђkЕФШЁжЕЗЖЮЇЪЧ_____ЃЛЂкШєfЃЈxЃЉЕФжЕгђЮЊRЃЌдђkЕФШЁжЕЗЖЮЇЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЫФРтзЖP-ABCDжаЃЌЕзУцABCDЮЊжБНЧЬнаЮЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЧвЦНУц
ЃЌЧвЦНУц![]() ЦНУцABCD.
ЦНУцABCD.
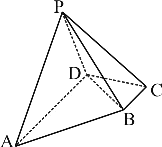
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉдкЯпЖЮPAЩЯЪЧЗёДцдквЛЕуMЃЌЪЙЖўУцНЧM-BC-DЕФДѓаЁЮЊ![]() ЃПШєДцдкЃЌЧѓГі
ЃПШєДцдкЃЌЧѓГі![]() ЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєЫФУцЬхABCDЕФШ§зщЖдРтЗжБ№ЯрЕШЃЌМДABЃНCDЃЌACЃНBDЃЌADЃНBCЃЌдђЯТСаНсТле§ШЗЕФЪЧЃЈ ЃЉ
A.ЫФУцЬхABCDУПзщЖдРтЯрЛЅДЙжБ
B.ЫФУцЬхABCDУПИіУцЕФУцЛ§ЯрЕШ
C.ДгЫФУцЬхABCDУПИіЖЅЕуГіЗЂЕФШ§ЬѕРтСНСНМаНЧжЎКЭДѓгк90ЁуЧваЁгк180Ёу
D.СЌНгЫФУцЬхABCDУПзщЖдРтжаЕуЕФЯпЖЮЯрЛЅДЙжБЦНЗж
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЖрУцЬх![]() жаЃЌЕзУц
жаЃЌЕзУц![]() ЮЊСтаЮЃЌ
ЮЊСтаЮЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЧвЦНУц
ЃЌЧвЦНУц![]() ЕзУц
ЕзУц![]() ЃЌЦНУц
ЃЌЦНУц![]() ЕзУц
ЕзУц![]() ЃЎ
ЃЎ
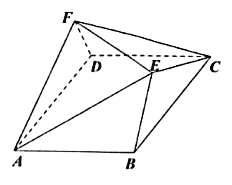
ЃЈ1ЃЉжЄУїЃК![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓЖўУцНЧ![]() ЕФгрЯвжЕЃЎ
ЕФгрЯвжЕЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com