
【题目】已知圆![]() ,直线
,直线![]() .
.
(1)若直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
(2)若![]() 是直线
是直线![]() 上的动点,过
上的动点,过![]() 作圆
作圆![]() 的两条切线
的两条切线![]() ,切点为
,切点为![]() ,探究:直线
,探究:直线![]() 是否过定点;
是否过定点;
(3)若![]() 为圆
为圆![]() 的两条相互垂直的弦,垂足为
的两条相互垂直的弦,垂足为![]() ,求四边形
,求四边形![]() 的面积的最大值.
的面积的最大值.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]()
【解析】
试题分析:(1)依题意圆O的半径![]() =
=![]() ,点O到
,点O到![]() 的距离
的距离![]() ,即
,即![]() =
=![]() ·
·![]() ,所以
,所以![]() ;(2)由题意O、P、C、D四点共圆且在以OP为直径的圆上,设
;(2)由题意O、P、C、D四点共圆且在以OP为直径的圆上,设![]() ,则得
,则得![]() ,即
,即![]() ,而C、D在圆O:
,而C、D在圆O:![]() 上,所以CD方程为
上,所以CD方程为![]() ,整理得
,整理得![]() ,由
,由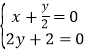 得
得![]() ,故直线CD过定点
,故直线CD过定点![]() ;(3)设圆心到EF、GH的距离分别为
;(3)设圆心到EF、GH的距离分别为![]() ,则
,则![]() , 而
, 而![]() ,
,![]() ,
,![]() ,
,
故![]() , 当且仅当
, 当且仅当![]() 即
即![]() 时,取“=”.
时,取“=”.
试题解析:(1)![]() 点O到
点O到![]() 的距离
的距离![]() 2(分)
2(分)
∴![]() =
=![]() ·
·![]()
![]()
![]() (4分)
(4分)
(2)由题意可知:O、P、C、D四点共圆且在以OP为直径的圆上,设![]()
其方程为:![]()
即:![]()
又C、D在圆O:![]() 上
上
∴![]() 即
即![]() (7分)
(7分)
由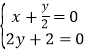 得
得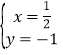
∴直线CD过定点![]() (9分)
(9分)
(3)设圆心O到直线EF、GH的距离分别为![]() .
.
则![]() (11分)
(11分)
∴![]()
![]()
∴![]()
当且仅当![]() 即
即![]() 时,取“=”
时,取“=”
∴四边形EGFH的面积的最大值为![]() (14分)
(14分)


科目:高中数学 来源: 题型:
【题目】某校100名学生期中考试数学成绩的频率分布直方图如图:
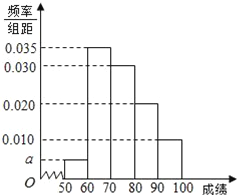
(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均分;
(3)现用分层抽样的方法从第3、4、5组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知公比不为1的等比数列{an}的前3项积为27,且2a2为3a1和a3的等差中项.
(1)求数列{an}的通项公式an;
(2)若数列{bn}满足bn=bn﹣1log3an+1(n≥2,n∈N*),且b1=1,求数列{ ![]() }的前n项和Sn .
}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了节约用水,学校改革澡堂收费制度,实行计时收费,洗澡时间在30分钟以内(含30分钟),每分钟收费0.1元,30分钟以上超出的部分每分钟0.2元,请设计程序,使用基本语句完成澡堂计费工作,要求输入时间,输出费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|ax﹣1|
(1)若f(x)≤2的解集为[﹣3,1],求实数a的值;
(2)若a=1,若存在x∈R,使得不等式f(2x+1)﹣f(x﹣1)≤3﹣2m成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设 ![]() ,
, ![]() ,
, ![]() 均为非零向量,已知命题p:
均为非零向量,已知命题p: ![]() =
= ![]() 是
是 ![]()
![]() =
= ![]()
![]() 的必要不充分条件,命题q:x>1是|x|>1成立的充分不必要条件,则下列命题是真命题的是( )
的必要不充分条件,命题q:x>1是|x|>1成立的充分不必要条件,则下列命题是真命题的是( )
A.p∧q
B.p∨q
C.(¬p)∧(¬q)
D.p∨(¬q)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知常数![]() 数列
数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() 且
且![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() 且数列
且数列![]() 是单调递增数列,求实数
是单调递增数列,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 数列
数列![]() 满足:
满足:![]() 对于任意给定的正整数
对于任意给定的正整数![]() ,是否存在
,是否存在![]() 使
使![]() ?若存在,求
?若存在,求![]() 的值(只要写出一组即可);若不存在,说明理由.
的值(只要写出一组即可);若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面内动点P与点A(﹣3,0)和点B(3,0)的连线的斜率之积为﹣ ![]() .
.
(1)求动点P的轨迹方程;
(2)设点P的轨迹且曲线C,过点(1,0)的直线与曲线C交于M,N两点,记△AMB的面积为S1 , △ANB的面积为S2 , 当S1﹣S2取得最大值时,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的顶点
的顶点![]() ,
, ![]() 边上的中线
边上的中线![]() 所在的直线方程为
所在的直线方程为![]() ,
, ![]() 边上的高
边上的高![]() 所在直线的方程为
所在直线的方程为![]() .
.
(![]() )求
)求![]() 的顶点
的顶点![]() 、
、![]() 的坐标.
的坐标.
(![]() )若圆
)若圆![]() 经过不同的三点
经过不同的三点![]() 、
、![]() 、
、![]() ,且斜率为
,且斜率为![]() 的直线与圆
的直线与圆![]() 相切于点
相切于点![]() ,求圆
,求圆![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com