
【题目】随着网络的发展,人们可以在网络上购物、玩游戏、聊天、导航等,所以人们对上网流量的需求越来越大。某电信运营商推出一款新的“流量包”套餐.为了调查不同年龄的人是否愿意选择此款“流量包”套餐,随机抽取50个用户按年龄分组进行访谈,统计结果如下表.
组号 | 年龄 | 访谈人数 | 愿意使用 |
1 | [20,30) | 5 | 5 |
2 | [30.40) | 10 | 10 |
3 | [40.50) | 15 | 12 |
4 | [50.60) | 14 | 8 |
5 | [60,70) | 6 | 2 |
(1)若在第2、3、4组愿意选择此款“流量包”套餐的人中,用分层抽样的方法抽取15人,则各组应分别抽取多少人?
(2)若从第5组的被调查者访谈人中随机选取2人进行追踪调查,求2人中至少有1人愿意选择此款“流量包”套餐的概率.
(3)按以上统计数据填写下面2×2列联表,并判断以50岁为分界点,能否在犯错误不超过1%的前提下认为是否愿意选择此款“流量包”套餐与人的年龄有关;
年龄不低于50岁的人数 | 年龄低于50岁的人数 | 合计 | ||||||||
愿意使用的人数 | ||||||||||
不愿意使用的人数 | ||||||||||
合计 |
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【答案】(1)各组分别为5人,6人,4人;(2)![]() ;(3)在犯错误不超过1%的前提下认为是否愿意选择此款“流量包”套餐与人的年龄有关.
;(3)在犯错误不超过1%的前提下认为是否愿意选择此款“流量包”套餐与人的年龄有关.
【解析】试题分析:(1)三组一共有![]() 人,抽取
人,抽取![]() 人,故两个人抽一人,由此得到抽取的人数分别为
人,故两个人抽一人,由此得到抽取的人数分别为![]() 人.(2)利用列举法列举出所有可能性有
人.(2)利用列举法列举出所有可能性有![]() 种,其中符合题意的有
种,其中符合题意的有![]() 种,故概率为
种,故概率为![]() .(3)根据题意填写好表格后,计算
.(3)根据题意填写好表格后,计算![]() ,故有在犯错误不超过1%的前提下认为是否愿意选择此款“流量包”套餐与人的年龄有关.
,故有在犯错误不超过1%的前提下认为是否愿意选择此款“流量包”套餐与人的年龄有关.
试题解析:
解:(1)因为![]() ,所以第2、3、4组愿意选择此款“流量包”套餐的人中,用分层抽样的方法抽取15人,各组分别为5人,6人,4人.
,所以第2、3、4组愿意选择此款“流量包”套餐的人中,用分层抽样的方法抽取15人,各组分别为5人,6人,4人.
(2)设第5组中不愿意选择此款“流量包”套餐A,B,C,D,愿意选择此款“流量包”套餐人为a,b,则愿意从6人中选取2人有:![]() 共15个结果,其中至少有1人愿意选择此款“流量包”
共15个结果,其中至少有1人愿意选择此款“流量包”![]() 共9个结果,所以求2人中至少有1人愿意选择此款“流量包”套餐的概率
共9个结果,所以求2人中至少有1人愿意选择此款“流量包”套餐的概率![]() .
.
(3)2×2列联表
年龄不低于50岁的人数 | 年龄低于50岁的人数 | 合计 | |
使用的人数 | 10 | 27 | 37 |
不愿意使用的人数 | 10 | 3 | 13 |
合计 | 20 | 30 | 50 |
∴![]()
∴在犯错误不超过1%的前提下认为是否愿意选择此款“流量包”套餐与人的年龄有关.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:高中数学 来源: 题型:
【题目】电视连续剧《人民的名义》自2017年3月28日在湖南卫视开播以来,引发各方关注,收视率、点击率均占据各大排行榜首位.我们用简单随机抽样的方法对这部电视剧的观看情况进行抽样调查,共调查了600人,得到结果如下:其中图1是非常喜欢《人民的名义》这部电视剧的观众年龄的频率分布直方图;表1是不同年龄段的观众选择不同观看方式的人数.
观看方式 年龄(岁) | 电视 | 网络 |
| 150 | 250 |
| 120 | 80 |

![]()
求:(I)假设同一组中的每个数据用该组区间的中点值代替,求非常喜欢《人民的名义》这部电视剧的观众的平均年龄;
(II)根据表1,通过计算说明我们是否有99%的把握认为观看该剧的方式与年龄有关?
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附: 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,定义域为![]() 上的函数
上的函数![]() 是由一条射线及抛物线的一部分组成.利用该图提供的信息解决下面几个问题.
是由一条射线及抛物线的一部分组成.利用该图提供的信息解决下面几个问题.

(1)求![]() 的解析式;
的解析式;
(2)若![]() 关于的方程
关于的方程![]() 有三个不同解,求
有三个不同解,求![]() 的取值范围;
的取值范围;
(3)若![]() ,求
,求![]() 的取值集合.
的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}满足a2=2,a5=8.
(1)求{an}的通项公式;
(2)各项均为正数的等比数列{bn}中,b1=1,b2+b3=a4,求{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
极坐标系的极点为直角坐标系![]() 的原点,极轴为
的原点,极轴为![]() 轴的正半轴,两种坐标系中的长度单位相同,已知曲线
轴的正半轴,两种坐标系中的长度单位相同,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的直角坐标方程;
的直角坐标方程;
(2)直线 (
(![]() 为参数)与曲线
为参数)与曲线![]() 交于
交于![]() 两点,与
两点,与![]() 轴交于
轴交于![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中华人民共和国个人所得税》规定,公民月工资、薪金所得不超过3500元的部分不纳税,超过3500元的部分为全月纳税所得额,此项税款按下表分段累计计算:

已知张先生的月工资、薪金所得为10000元,问他当月应缴纳多少个人所得税?
设王先生的月工资、薪金所得为![]() 元,当月应缴纳个人所得税为
元,当月应缴纳个人所得税为![]() 元,写出
元,写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)已知王先生一月份应缴纳个人所得税为303元,那么他当月的个工资、薪金所得为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
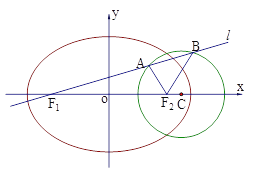
【题目】已知如图,圆![]() 、椭圆
、椭圆![]() 均经过点M
均经过点M![]() ,圆
,圆![]() 的圆心为
的圆心为![]() ,椭圆
,椭圆![]() 的两焦点分别为
的两焦点分别为![]() .
.
(Ⅰ)分别求圆![]() 和椭圆
和椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)过![]() 作直线
作直线![]() 与圆
与圆![]() 交于
交于![]() 、
、![]() 两点,试探究
两点,试探究![]() 是否为定值?若是定值,求出该定值;若不是,说明理由.
是否为定值?若是定值,求出该定值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在[-1,1]上的奇函数,当x∈[-1,0]时,函数的解析式为f(x)=![]() (a∈R).
(a∈R).
(1)试求a的值;
(2)写出f(x)在[0,1]上的解析式;
(3)求f(x)在[0,1]上的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com