
【题目】下面有命题:
①y=|sinx-![]() |的周期是2π;
|的周期是2π;
②y=sinx+sin|x|的值域是[0,2] ;
③方程cosx=lgx有三解;
④![]() 为正实数,
为正实数,![]() 在
在![]() 上递增,那么
上递增,那么![]() 的取值范围是
的取值范围是![]() ;
;
⑤在y=3sin(2x+![]() )中,若f(x
)中,若f(x![]() )=f(x2)=0,则x1-x2必为
)=f(x2)=0,则x1-x2必为![]() 的整数倍;
的整数倍;
⑥若A、B是锐角△ABC的两个内角,则点P(cosB-sinA,sinB-cosA)在第二象限;
⑦在![]() 中,若
中,若![]() ,则
,则![]() 钝角三角形。
钝角三角形。
其中真命题个数为( )
A. 2 B. 3 C. 4 D. 5
科目:高中数学 来源: 题型:
【题目】某城市在发展过程中,交通状况逐渐受到有关部门的关注,据有关统计数据显示,从上午6点到中午12点,车辆通过该市某一路段的用时y(分钟)与车辆进入该路段的时刻t之间的关系可近似地用如下函数给出: y= 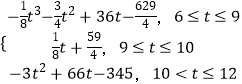
求从上午6点到中午12点,通过该路段用时最多的时刻.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四面体P﹣ABCD中,△ABD是边长为2的正三角形,PC⊥底面ABCD,AB⊥BP,BC= ![]() .
. 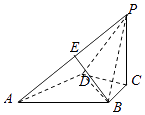
(1)求证:PA⊥BD;
(2)已知E是PA上一点,且BE∥平面PCD.若PC=2,求点E到平面ABCD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆C的两个焦点是F1、F2 , 过F1的直线与椭圆C交于P、Q,若|PF2|=|F1F2|,且5|PF1|=6|F1Q|,则椭圆的离心率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于空间两不同的直线![]() ,两不同的平面
,两不同的平面![]() ,有下列推理:
,有下列推理:
(1)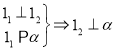 , (2)
, (2)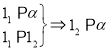 ,(3)
,(3)![]()
(4)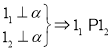 , (5)
, (5)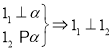
其中推理正确的序号为( )
A. (1)(3)(4) B. (2)(3)(5) C. (4)(5) D. (2)(3)(4)(5)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果函数![]() 在定义域内存在区间
在定义域内存在区间![]() ,使得该函数在区间
,使得该函数在区间![]() 上的值域为
上的值域为![]() ,则称函数
,则称函数![]() 是该定义域上的“和谐函数”.
是该定义域上的“和谐函数”.
(1)求证:函数![]() 是“和谐函数”;
是“和谐函数”;
(2)若函数![]() 是“和谐函数”,求实数
是“和谐函数”,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com