
【题目】随着经济的发展,个人收入的提高,自2019年1月1日起,个人所得税起征点和税率的调整.调整如下:纳税人的工资、薪金所得,以每月全部收入额减除5000元后的余额为应纳税所得额.依照个人所得税税率表,调整前后的计算方法如下表:
个人所得税税率表(调整前) | 个人所得税税率表(调整后) | ||||
免征额3500元 | 免征额5000元 | ||||
级数 | 全月应纳税所得额 | 税率(%) | 级数 | 全月应纳税所得额 | 税率(%) |
1 | 不超过1500元部分 | 3 | 1 | 不超过3000元部分 | 3 |
2 | 超过1500元至4500元的部分 | 10 | 2 | 超过3000元至12000元的部分 | 10 |
3 | 超过4500元至9000元的部分 | 20 | 3 | 超过12000元至25000元的部分 | 20 |
... | ... | ... | ... | ... | ... |
(1)假如小红某月的工资、薪金等所得税前收入总和不高于8000元,记![]() 表示总收入,
表示总收入,![]() 表示应纳的税,试写出调整前后
表示应纳的税,试写出调整前后![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)某税务部门在小红所在公司利用分层抽样方法抽取某月100个不同层次员工的税前收入,并制成下面的频数分布表:
收入(元) |
|
|
|
|
|
|
人数 | 30 | 40 | 10 | 8 | 7 | 5 |
①先从收入在![]() 及
及![]() 的人群中按分层抽样抽取7人,再从中选4人作为新纳税法知识宣讲员,用
的人群中按分层抽样抽取7人,再从中选4人作为新纳税法知识宣讲员,用![]() 表示抽到作为宣讲员的收入在
表示抽到作为宣讲员的收入在![]() 元的人数,
元的人数,![]() 表示抽到作为宣讲员的收入在
表示抽到作为宣讲员的收入在![]() 元的人数,随机变量
元的人数,随机变量![]() ,求
,求![]() 的分布列与数学期望;
的分布列与数学期望;
②小红该月的工资、薪金等税前收入为7500元时,请你帮小红算一下调整后小红的实际收入比调整前增加了多少?
【答案】(1)![]() ;(2)①详见解析,②220元.
;(2)①详见解析,②220元.
【解析】
(1)根据题意可列出纳税y与总收入x的关系式。
(2)根据分层抽样,求得![]() 及
及![]() 各自抽取人数。从中抽取4人,所以z的可能有三种。分别求这三种情况下的概率,结合分布列与数学期望的求法可得解。
各自抽取人数。从中抽取4人,所以z的可能有三种。分别求这三种情况下的概率,结合分布列与数学期望的求法可得解。
根据调整前后纳税计算公式,分别求得两种情况下的纳税额,求其差即可求得增加额。
解:(1)调整前![]() 关于
关于![]() 的表达式为
的表达式为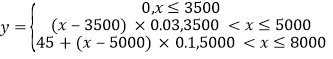 ,
,
调整后![]() 关于
关于![]() 的表达式为
的表达式为![]() .
.
(2)①由频数分布表可知从![]() 及
及![]() 的人群中抽取7人,其中
的人群中抽取7人,其中![]() 中占3人,
中占3人,![]() 的人中占4人,
的人中占4人,
再从这7人中选4人,所以![]() 的取值可能为0,2,4,
的取值可能为0,2,4,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
所以其分布列为
| 0 | 2 | 4 |
|
|
|
|
所以![]() .
.
②由于小红的工资、薪金等税前收入为7500元,
按调整起征点前应纳个税为![]() 元;
元;
按调整起征点后应纳个税为![]() 元,
元,
由此可知,调整起征点后应纳个税少交220元,
即个人的实际收入增加了220元,
所以小红的实际收入增加了220元.


科目:高中数学 来源: 题型:
【题目】某市教学研究室为了对今后所出试题的难度有更好的把握,提高命题质量,对该市高三理科数学试卷的得分情况进行了调研.从全市参加考试的理科考生中随机抽取了100名考生的数学成绩(满分150分),将数据分成9组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并整理得到如图所示的频率分布直方图.用统计的方法得到样本标准差
,并整理得到如图所示的频率分布直方图.用统计的方法得到样本标准差![]() ,以频率值作为概率估计值.
,以频率值作为概率估计值.

(Ⅰ)根据频率分布直方图,求抽取的100名理科考生数学成绩的平均分![]() 及众数
及众数![]() ;
;
(Ⅱ)用频率估计概率,从该市所有高三理科考生的数学成绩中随机抽取3个,记理科数学成绩位于区间![]() 内的个数为
内的个数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() ;
;
(Ⅲ)从该市高三理科数学考试成绩中任意抽取一份,记其成绩为![]() ,依据以下不等式评判(
,依据以下不等式评判(![]() 表示对应事件的概率):
表示对应事件的概率):
①![]() ,②
,②![]() ,
,
③![]() ,其中
,其中![]() .
.
评判规则:若至少满足以上两个不等式,则给予这套试卷好评,否则差评.试问:这套试卷得到好评还是差评?
查看答案和解析>>
科目:高中数学 来源: 题型:
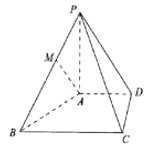
【题目】如图,在四棱锥![]() 中,
中,![]() ,底面四边形
,底面四边形![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一点.
上一点.
(1)若![]() ,则在线段
,则在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,请确定
?若存在,请确定![]() 点的位置;若不存在,请说明理由
点的位置;若不存在,请说明理由
(2)己知![]() ,若异面直线
,若异面直线![]() 与
与![]() 成
成![]() 角,二而角
角,二而角![]() 的余弦值为
的余弦值为![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD的底面ABCD为正方形,![]() ,E,F分别是棱PC,AB的中点.
,E,F分别是棱PC,AB的中点.
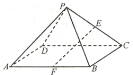
(1)求证:![]() 平面PAD;
平面PAD;
(2)若![]() ,求直线EF与平面PAB所成角的正弦值.
,求直线EF与平面PAB所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,直线
,直线![]() 上有两点E,F使
上有两点E,F使![]() ,点P在线段
,点P在线段![]() 的延长线上,且
的延长线上,且![]() .
.
(1)若![]() ,求点P的轨迹方程;
,求点P的轨迹方程;
(2)若在点P的轨迹上存在两点M,N,设![]() ,
,![]() 的夹角为
的夹角为![]() .
.
①若![]() ,求证:直线
,求证:直线![]() 过定点,并求定点坐标;
过定点,并求定点坐标;
②若![]() 为锐角,求直线
为锐角,求直线![]() 与x轴交点横坐标的取值范围.
与x轴交点横坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将![]() 方格表的每个方格任意填入
方格表的每个方格任意填入![]() 或
或![]() ,然后允许进行如下操作:每次任意选择一行(或列),将这一行(或列)中的数全部变号.若无论开始时方格表的数怎样填,总能经过不超过
,然后允许进行如下操作:每次任意选择一行(或列),将这一行(或列)中的数全部变号.若无论开始时方格表的数怎样填,总能经过不超过![]() 次操作,使得方格表每一行中所有数的和、每一列中所有数的和均非负.试确定
次操作,使得方格表每一行中所有数的和、每一列中所有数的和均非负.试确定![]() 的最小值
的最小值![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com