分析:(1)连接B1P,假设B1P⊥平面ACC1A1,根据线面垂直的性质定理可知∠B1A1C1=90°,这与△A1B1C1是等边三角形矛盾,所以B1P不可能与平面ACC1A1垂直;
(2)取A1B1的中点D,连接C1D、BD、BC1,先求出AP长,连接B1C,交BC1于点O,过O在平面CPB1上作OE⊥B1P,交B1P于点E,连接C1E,根据二面角的定义证得∠OEC1是二面角C-B1P-C1的平面角,在三角形OEC1中求出此角即可.
解答:解:
(1)证明:连接B
1P,假设B
1P⊥平面ACC
1A
1,则B
1P⊥A
1C
1.
由于三棱柱ABC-A
1B
1C
1为正三棱柱,
∴AA
1⊥A
1C
1.
∴A
1C
1⊥侧面ABB
1A
1.
∴A
1C
1⊥A
1B
1,
即∠B
1A
1C
1=90°.
这与△A
1B
1C
1是等边三角形矛盾.
∴B
1P不可能与平面ACC
1A
1垂直.
(2)取A
1B
1的中点D,连接C
1D、BD、BC
1,
则C
1D⊥A
1B
1,又∵AA
1⊥平面A
1B
1C
1,
∴AA
1⊥C
1D.∴C
1D⊥平面ABB
1A
1.
∴BD是BC
1在平面ABB
1A
1上的射影.
∵BC
1⊥B
1P,∴BD⊥B
1P.∴∠B
1BD=90°-∠BB
1P=∠A
1B
1P.
又A
1B
1=B
1B=2,∴△BB
1D≌△B
1A
1P,A
1P=B
1D=1.∴AP=1.
连接B
1C,交BC
1于点O,则BC
1⊥B
1C.
又BC
1⊥B
1P,∴BC
1⊥平面B
1CP.
过O在平面CPB
1上作OE⊥B
1P,交B
1P于点E,
连接C
1E,则B
1P⊥C
1E,
∴∠OEC
1是二面角C-B
1P-C
1的平面角.
由于CP=B
1P=
,O为B
1C的中点,连接OP,
∴PO⊥B
1C,OP•OB
1=OE•B
1P.∴OE=
.
∴tan∠OEC
1=
=
.
∴∠OEC
1=arctan
.
故二面角C-B
1P-C
1的大小为arctan
.
点评:本题主要考查了直线与平面的位置关系,以及二面角等有关知识,考查空间想象能力、运算能力和推理论证能力,属于基础题.

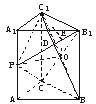
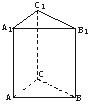 如图,正三棱柱ABC-A1B1C1的所有棱长均为2,P是侧棱AA1上任意一点.
如图,正三棱柱ABC-A1B1C1的所有棱长均为2,P是侧棱AA1上任意一点. (1)证明:连接B1P,假设B1P⊥平面ACC1A1,则B1P⊥A1C1.
(1)证明:连接B1P,假设B1P⊥平面ACC1A1,则B1P⊥A1C1.

 名校通行证有效作业系列答案
名校通行证有效作业系列答案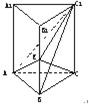 如图,正三棱柱ABC-A1B1C1各棱长都等于a,E是BB1的中点.
如图,正三棱柱ABC-A1B1C1各棱长都等于a,E是BB1的中点. (2013•郑州二模)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
(2013•郑州二模)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.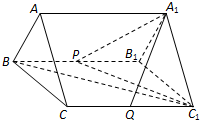 如图,正三棱柱ABC-A1B1C1中(注:底面为正三角形且侧棱与底面垂直),BC=CC1=2,P,Q分别为BB1,CC1的中点.
如图,正三棱柱ABC-A1B1C1中(注:底面为正三角形且侧棱与底面垂直),BC=CC1=2,P,Q分别为BB1,CC1的中点.