
【题目】已知函数f(x)=2|x+1|+|x﹣a|(a∈R).
(1)若 a=1,求不等式 f(x)≥5的解集;
(2)若函数f(x)的最小值为3,求实数 a的值.
【答案】
(1)解:当 a=1, 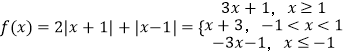 ,当x≥1时,3x+1≥5,即
,当x≥1时,3x+1≥5,即 ![]() ,∴
,∴ ![]() ;
;
当﹣1<x<1时,x+3≥5,即x≥2,此时x无实数解;
当x≤﹣1时,﹣3x﹣1≥5,即x≤﹣2,∴x≤﹣2.
综上所述,不等式的解集为{x|x≤﹣2,或 ![]() .
.
(2)解:当a=﹣1时,f(x)=3|x+1|最小值为 0,不符合题意,
当a>﹣1时, 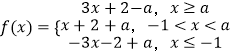 ,∴f(x)min=f(﹣1)=1+a=3,此时a=2;
,∴f(x)min=f(﹣1)=1+a=3,此时a=2;
当a<﹣1时, 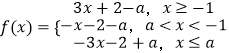 ,f(x)min=f(﹣1)=﹣1﹣a=3,此时a=﹣4.
,f(x)min=f(﹣1)=﹣1﹣a=3,此时a=﹣4.
综上所示,a=2或a=﹣4.
【解析】(1)把f(x)写成分段函数的形式,分类讨论,分别求得不等式 f(x)≥5的解集,综合可得结论.(2)分当a=﹣1时、当a>﹣1时、当a<﹣1时三种情况,分别求得a的值,综合可得结论.
【考点精析】本题主要考查了绝对值不等式的解法的相关知识点,需要掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知函数 f(x)=loga(x+1)﹣loga(1﹣x),a>0 且 a≠1.
(1)判断 f(x)的奇偶性并予以证明;
(2)当 a>1 时,求使 f(x)>0 的 x 的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线C:x2=4y,点P是C的准线l上的动点,过点P作C的两条切线,切点分别为A,B,则△AOB面积的最小值为( )
A.![]()
B.2
C.2 ![]()
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,给出如下命题:
中,给出如下命题:
①![]() 是
是![]() 所在平面内一定点,且满足
所在平面内一定点,且满足![]() ,则
,则![]() 是
是![]() 的垂心;
的垂心;
②![]() 是
是![]() 所在平面内一定点,动点
所在平面内一定点,动点![]() 满足
满足![]() ,
,![]() ,则动点
,则动点![]() 一定过
一定过![]() 的重心;
的重心;
③![]() 是
是![]() 内一定点,且
内一定点,且![]() ,则
,则![]() ;
;
④若 且
且 ,则
,则![]() 为等边三角形,
为等边三角形,
其中正确的命题为_____(将所有正确命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,点 P的极坐标是 ![]() ,曲线 C的极坐标方程为
,曲线 C的极坐标方程为 ![]() .以极点为坐标原点,极轴为 x轴的正半轴建立平面直角坐标系,斜率为﹣1的直线 l经过点P.
.以极点为坐标原点,极轴为 x轴的正半轴建立平面直角坐标系,斜率为﹣1的直线 l经过点P.
(1)写出直线 l的参数方程和曲线 C的直角坐标方程;
(2)若直线 l和曲线C相交于两点A,B,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最小正周期为
的最小正周期为![]() ,且直线
,且直线![]() 是其图象的一条对称轴.
是其图象的一条对称轴.
(1)求函数![]() 的解析式;
的解析式;
(2)在![]() 中,角
中,角![]() 、
、![]() 、
、![]() 所对的边分别为
所对的边分别为![]() 、
、![]() 、
、![]() ,且
,且![]() ,
,![]() ,若
,若![]() 角满足
角满足![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位,再将所得的图象上每一点的纵坐标不变,横坐标伸长为原来的
个单位,再将所得的图象上每一点的纵坐标不变,横坐标伸长为原来的![]() 倍后所得到的图象对应的函数记作
倍后所得到的图象对应的函数记作![]() ,已知常数
,已知常数![]() ,
,![]() ,且函数
,且函数![]() 在
在![]() 内恰有
内恰有![]() 个零点,求常数
个零点,求常数![]() 与
与![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一家面包房根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图,如图231所示.
 图231
图231
将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
(1)求在未来连续3天里,有连续2天的日销售量都不低于100个且另1天的日销售量低于50个的概率;
(2)用X表示在未来3天里日销售量不低于100个的天数,求随机变量X的分布列,期望E(X)及方差D(X).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com