
为了解某校学生的视力情况,现采用随机抽样的方式从该校的A,B两班中各抽5名学生进行视力检测.检测的数据如下:
A班5名学生的视力检测结果:4.3,5.1,4.6,4.1,4.9.
B班5名学生的视力检测结果:5.1,4.9,4.0,4.0,4.5.
(1)分别计算两组数据的平均数,从计算结果看,哪个班的学生视力较好?
(2)由数据判断哪个班的5名学生视力方差较大?(结论不要求证明)
(3) 现从A班的上述5名学生中随机选取3名学生,用X表示其中视力大于4.6的人数,求X的分布列和数学期望.
(1)A班学生的视力较好;(2)B班5名学生视力的方差较大;(3)所以随机变量 的分布列如下:
的分布列如下:
0 1 2 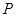
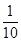
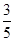
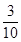
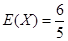 .
.
解析试题分析:(1)计算出平均数,看平均数的大小,平均数大的班学生的视力较好;(2)对数据分析,一看极差,二看数据集中程度,越集中方差越小,越离散方差越大,从数据上看,B班5名学生视力极差较大,数据相对较散,从而的结论;(3)对数据观察,找出视力大于4.6的人数,从而确定出 的所有可能取值,分别求出它们的概率,得分布列,进而可求出期望.
的所有可能取值,分别求出它们的概率,得分布列,进而可求出期望.
(1) A班5名学生的视力平均数为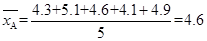 , 2分
, 2分
B班5名学生的视力平均数为 . 3分
. 3分
从数据结果来看A班学生的视力较好. 4分
(2)B班5名学生视力的方差较大. 7分
(3)由(1)知,A班的5名学生中有2名学生视力大于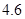 .
.
则 的所有可能取值为
的所有可能取值为 ,
,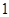 ,
, . 8分
. 8分
所以 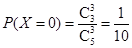 ; 9分
; 9分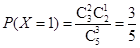 ; 10分
; 10分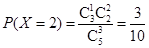 . 11分
. 11分
所以随机变量 的分布列如下:
的分布列如下:
12分
0 1 2 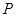
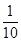
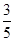
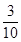
故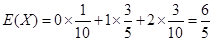 . 13分
. 13分
考点:统计数据分析,平均数,方差,分布列与期望.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下:请观察图形,求解下列问题:
(1)79.5~89.5这一组的频率、频数分别是多少?
(2)估计这次环保知识竞赛的及格率(60分及以上为及格)和平均分.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某中学的数学测试中设置了“数学与逻辑”和“阅读与表达”两个内容,成绩分为A、B、C、D、E五个等级。某班考生两科的考试成绩的数据统计如图所示,其中“数学与逻辑”科目的成绩等级为B的考生有10人
(1)求该班考生中“阅读与表达”科目中成绩等级为A的人数;
(2)若等级A、B、C、D、E分别对应5分、4分、3分、2分、1分,该考场中有2人10分,3人9分,从这5人中随机抽取2人,求2人成绩之和为19分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某数学兴趣小组有男女生各 名.以下茎叶图记录了该小组同学在一次数学测试中的成绩(单位:分).已知男生数据的中位数为
名.以下茎叶图记录了该小组同学在一次数学测试中的成绩(单位:分).已知男生数据的中位数为 ,女生数据的平均数为
,女生数据的平均数为 .
.
(1)求 ,
, 的值;
的值;
(2)现从成绩高于 分的同学中随机抽取两名同学,求抽取的两名同学恰好为一男一女的概率.
分的同学中随机抽取两名同学,求抽取的两名同学恰好为一男一女的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
“你低碳了吗?”这是某市为倡导建设资源节约型社会而发布的公益广告里的一句话.活动组织者为了解这则广告的宣传效果,随机抽取了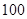 名年龄段在
名年龄段在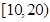 ,
,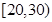 ,
,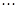 ,
,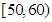 的市民进行问卷调查,由此得到样本的频率分布直方图如图所示.
的市民进行问卷调查,由此得到样本的频率分布直方图如图所示.
(1)求随机抽取的市民中年龄段在 的人数;
的人数;
(2)从不小于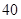 岁的人中按年龄段分层抽样的方法随机抽取
岁的人中按年龄段分层抽样的方法随机抽取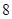 人,求
人,求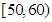 年龄段抽取的人数;
年龄段抽取的人数;
(3)从按(2)中方式得到的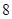 人中再抽取3人作为本次活动的获奖者,记
人中再抽取3人作为本次活动的获奖者,记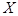 为年龄在
为年龄在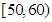 年龄段的人数,求
年龄段的人数,求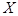 的分布列及数学期望.
的分布列及数学期望.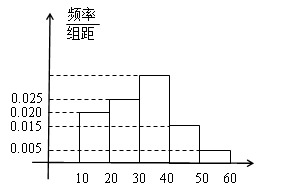
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
2013年11月,青岛发生输油管道爆炸事故造成胶州湾局部污染.国家海洋局用分层抽样的方法从国家环保专家、海洋生物专家、油气专家三类专家库中抽取若干人组成研究小组赴泄油海域工作,有关数据见表1(单位:人)
海洋生物专家为了检测该地受污染后对海洋动物身体健康的影响,随机选取了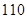 只海豚进行了检测,并将有关数据整理为不完整的
只海豚进行了检测,并将有关数据整理为不完整的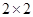 列联表,如表2.
列联表,如表2.
(1)求研究小组的总人数;
(2)写出表2中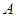 、
、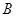 、
、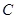 、
、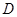 、
、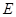 的值,并判断有多大的把握认为海豚身体不健康与受到污染有关;
的值,并判断有多大的把握认为海豚身体不健康与受到污染有关;
(3)若从研究小组的环保专家和海洋生物专家中随机选 人撰写研究报告,求其中恰好有
人撰写研究报告,求其中恰好有 人为环保专家的概率.
人为环保专家的概率.
附:①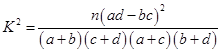 ,其中
,其中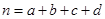 .
.
②
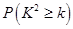 | 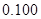 | 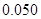 | 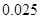 | 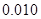 | 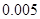 | 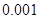 |
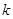 | 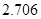 | 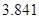 | 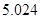 | 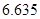 |  | 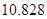 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
学校从参加高一年级期中考试的学生中抽出50名学生,并统计了他们的数学成绩(成绩均为整数且满分为100分),数学成绩分组及各组频数如下:
[40,50),2;[50,60),3;[60,70),14;[70,80),15;[80,90),12;[90,100],4.
(1)在给出的样本频率分布表中,求A,B,C,D的值;
(2)估计成绩在80分以上(含80分)学生的比例;
(3)为了帮助成绩差的学生提高数学成绩,学校决定成立“二帮一”小组,即从成绩在[90,100]的学生中选两位同学,共同帮助成绩在[40,50)中的某一位同学.已知甲同学的成绩为42分,乙同学的成绩为95分,求甲、乙两同学恰好被安排在同一小组的概率.样本频率分布表如下:
| 分组 | 频数 | 频率 |
| [40,50) | 2 | 0.04 |
| [50,60) | 3 | 0.06 |
| [60,70) | 14 | 0.28 |
| [70,80) | 15[] | 0.30 |
| [80,90) | A | B |
| [90,100] | 4 | 0.08 |
| 合计 | C | D |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分 )
2013年国庆期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段 ,
, ,
, ,
, ,
, ,
, 后得到如下图的频率分布直方图.
后得到如下图的频率分布直方图.
(1)此调查公司在采样中,用到的是什么抽样方法?
(2)求这40辆小型车辆车速的中位数的估计值;
(3)若从车速在 的车辆中任抽取3辆,求抽出的3辆车中车速在
的车辆中任抽取3辆,求抽出的3辆车中车速在 的车辆数
的车辆数 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂生产 、
、 两种元件,其质量按测试指标划分为:大于或等于
两种元件,其质量按测试指标划分为:大于或等于 为正品,小于
为正品,小于 为次品.现从一批产品中随机抽取这两种元件各
为次品.现从一批产品中随机抽取这两种元件各 件进行检测,检测结果记录如下:
件进行检测,检测结果记录如下:
 |  |  |  |  |  |
| B |  |  |  |  |  |
 、
、 看不清,统计员只记得
看不清,统计员只记得 ,且
,且 、
、 两种元件的检测数据的平均值相等,方差也相等.
两种元件的检测数据的平均值相等,方差也相等. 与
与 的值;
的值; 件
件 种元件中任取
种元件中任取 件,求
件,求 件都为正品的概率.
件都为正品的概率.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com