
【题目】已知:三棱柱![]() 中,底面是正三角形,侧棱
中,底面是正三角形,侧棱![]() 面
面![]() ,
, ![]() 是棱
是棱![]() 的中点,点
的中点,点![]() 在棱
在棱![]() 上,且
上,且![]() .
.
(![]() )求证:
)求证: ![]() 平面
平面![]() .
.
(![]() )求证:
)求证: ![]() .
.

【答案】(1)见解析(2)见解析
【解析】试题分析:(1)设![]() 与
与![]() 交点为
交点为![]() ,则根据三角形中位线性质得
,则根据三角形中位线性质得![]() ,再利用线面平行判定定理得结论(2)
,再利用线面平行判定定理得结论(2)![]() 面
面![]() 得
得![]() ,再由正三角形性质得
,再由正三角形性质得![]() ,因此由线面垂直判定定理得
,因此由线面垂直判定定理得![]() 平面
平面![]() ,即
,即![]() ,再结合条件
,再结合条件![]() ,利用线面垂直判定定理得
,利用线面垂直判定定理得![]() 平面
平面![]() ,即得
,即得![]() .
.
试题解析:(![]() )证明:连接
)证明:连接![]() ,
,
设![]() 与
与![]() 交点为
交点为![]() ,连接
,连接![]() ,
,
∵在![]() 中,
中,
![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 中点,
中点,
∴![]() ,
,
∵![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(![]() )∵
)∵![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
∴![]() ,
,
∵在正![]() 中,
中,
![]() 是棱
是棱![]() 中点,
中点,
∴![]() ,
,
∵![]() 点,
点,
![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() ,
,
又∵![]() ,
,
![]() 点,
点,
![]() 、
、![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() .
.

点睛:垂直、平行关系证明中应用转化与化归思想的常见类型.
(1)证明线面、面面平行,需转化为证明线线平行.
(2)证明线面垂直,需转化为证明线线垂直.
(3)证明线线垂直,需转化为证明线面垂直.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点
的焦点![]() 在直线
在直线![]() 上,且抛物线
上,且抛物线![]() 截直线
截直线![]() 所得的弦
所得的弦![]() 的长为
的长为![]() .
.
(Ⅰ)求抛物线![]() 的方程和
的方程和![]() 的值.
的值.
(Ⅱ)以弦![]() 为底边,以
为底边,以![]() 轴上点
轴上点![]() 为顶点的三角形
为顶点的三角形![]() 面积为
面积为![]() ,求点
,求点![]() 坐标.
坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知圆![]() 的极坐标方程为
的极坐标方程为![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴的正半轴建立平面直角坐标系,取相同单位长度(其中
轴的正半轴建立平面直角坐标系,取相同单位长度(其中![]() ,
, ![]() ),若倾斜角为
),若倾斜角为![]() 且经过坐标原点的直线
且经过坐标原点的直线![]() 与圆
与圆![]() 相交于点
相交于点![]() (
(![]() 点不是原点).
点不是原点).
(1)求点![]() 的极坐标;
的极坐标;
(2)设直线![]() 过线段
过线段![]() 的中点
的中点![]() ,且直线
,且直线![]() 交圆
交圆![]() 于
于![]() 两点,求
两点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在“新零售”模式的背景下,某大型零售公司咪推广线下分店,计划在![]() 市的
市的![]() 区开设分店,为了确定在该区开设分店的个数,该公司对该市已开设分店听其他区的数据作了初步处理后得到下列表格.记
区开设分店,为了确定在该区开设分店的个数,该公司对该市已开设分店听其他区的数据作了初步处理后得到下列表格.记![]() 表示在各区开设分店的个数,
表示在各区开设分店的个数, ![]() 表示这个
表示这个![]() 个分店的年收入之和.
个分店的年收入之和.
| 2 | 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 | 6 |
(1)该公司已经过初步判断,可用线性回归模型拟合![]() 与
与![]() 的关系,求
的关系,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)假设该公司在![]() 区获得的总年利润
区获得的总年利润![]() (单位:百万元)与
(单位:百万元)与![]() 之间的关系为
之间的关系为![]() ,请结合(1)中的线性回归方程,估算该公司应在
,请结合(1)中的线性回归方程,估算该公司应在![]() 区开设多少个分时,才能使
区开设多少个分时,才能使![]() 区平均每个分店的年利润最大?
区平均每个分店的年利润最大?
(参考公式: ![]() ,其中
,其中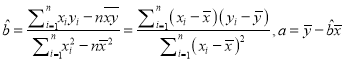 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系中,动圆![]() 与圆
与圆![]() 外切,且与直线
外切,且与直线![]() 相切,记圆心
相切,记圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)设过定点![]() (
(![]() 为非零常数)的动直线
为非零常数)的动直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,问:在曲线
两点,问:在曲线![]() 上是否存在点
上是否存在点![]() (与
(与![]() 两点相异),当直线
两点相异),当直线![]() 的斜率存在时,直线
的斜率存在时,直线![]() 的斜率之和为定值.若存在,求出点
的斜率之和为定值.若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin ![]() cos
cos ![]() ﹣2
﹣2 ![]() sin2
sin2 ![]() +
+ ![]()
(1)求函数f(x)的单调减区间
(2)已知α∈( ![]() ,
, ![]() ),且f(α)=
),且f(α)= ![]() ,求f(
,求f( ![]() )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温和平均最低气温的雷达图. 图中A点表示十月的平均最高气温约为![]() ,B点表示四月的平均最低气温约为
,B点表示四月的平均最低气温约为![]() . 下面叙述不正确的是 ( )
. 下面叙述不正确的是 ( )

A. 各月的平均最低气温都在![]() 以上
以上
B. 七月的平均温差比一月的平均温差大
C. 三月和十一月的平均最高气温基本相同
D. 平均最高气温高于![]() 的月份有5个
的月份有5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com