
【题目】在直角坐标系![]() 中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为
中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为![]() ,曲线C的极坐标方程为
,曲线C的极坐标方程为![]() .
.
(Ⅰ)求直线l和曲线C的直角坐标方程;
(Ⅱ)点M为曲线C上一点,求M到直线l的最小距离.
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,已知![]() 的两顶点坐标
的两顶点坐标![]() ,
,![]() ,圆
,圆![]() 是
是![]() 的内切圆,在边
的内切圆,在边![]() ,
,![]() ,
,![]() 上的切点分别为
上的切点分别为![]() ,
,![]() ,
,![]() ,
,![]() .
.
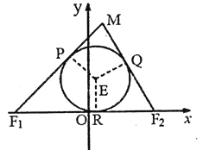
(Ⅰ)求证:![]() 为定值,并求出动点
为定值,并求出动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过![]() 的斜率不为零直线交曲线
的斜率不为零直线交曲线![]() 于
于![]() 、
、![]() 两点,求证:
两点,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆C:![]() 的左、右顶点分别为
的左、右顶点分别为![]() 右焦点为
右焦点为![]() ,右准线l的方程为
,右准线l的方程为![]() ,过焦点F的直线与椭圆C相交于点A,B(不与点
,过焦点F的直线与椭圆C相交于点A,B(不与点![]() 重合).
重合).
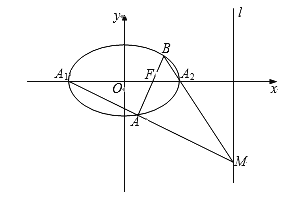
(1)求椭圆C的标准方程;
(2)当直线AB的倾斜角为45°时,求弦AB的长;
(3)设直线![]() 交l于点M,求证:B,
交l于点M,求证:B,![]() ,M三点共线.
,M三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】两个数列![]() 、
、![]() ,当
,当![]() 和
和![]() 同时在
同时在![]() 时取得相同的最大值,我们称
时取得相同的最大值,我们称![]() 与
与![]() 具有性质
具有性质![]() ,其中
,其中![]() .
.
(1)设![]() 的二项展开式中
的二项展开式中![]() 的系数为
的系数为![]() (
(![]() ),
),![]() ,记
,记![]() ,
,![]() ,
,![]() ,依次下去,
,依次下去,![]() ,组成的数列是
,组成的数列是![]() ;同样地,
;同样地,![]() 的二项展开式中
的二项展开式中![]() 的系数为
的系数为![]() (
(![]() ),
),![]() ,记
,记![]() ,
,![]() ,
,![]() ,依次下去,
,依次下去,![]() ,组成的数列是
,组成的数列是![]() ;判别
;判别![]() 与
与![]() 是否具有性质
是否具有性质![]() ,请说明理由;
,请说明理由;
(2)数列![]() 的前
的前![]() 项和是
项和是![]() ,数列
,数列![]() 的前
的前![]() 项和是
项和是![]() ,若
,若![]() 与
与![]() 具有性质
具有性质![]() ,
,![]() ,则这样的数列
,则这样的数列![]() 一共有多少个?请说明理由;
一共有多少个?请说明理由;
(3)两个有限项数列![]() 与
与![]() 满足
满足![]() ,
,![]() ,且
,且![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() 与
与![]() 具有性质
具有性质![]() ,请说明理由.
,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点![]() 分别为椭圆
分别为椭圆![]() 的左右顶点和右焦点,过点
的左右顶点和右焦点,过点![]() 的直线交椭圆
的直线交椭圆![]() 于点
于点![]() .
.
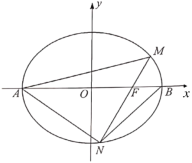
(1)若![]() ,点
,点![]() 与椭圆
与椭圆![]() 左准线的距离为
左准线的距离为![]() ,求椭圆
,求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 的斜率是直线
的斜率是直线![]() 斜率的
斜率的![]() 倍.
倍.
①求椭圆![]() 的离心率;
的离心率;
②若椭圆![]() 的焦距为
的焦距为![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省2020年高考将实施新的高考改革方案.考生的高考总成绩由3门统一高考科目成绩和自主选择的3门普通高中学业水平等级考试科目成绩组成,总分为750分.其中,统一高考科目为语文、数学、外语,自主选择的3门普通高中学业水平等级考试科目是从物理、化学、生物、政治、历史、地理6科中选择3门作为选考科目,语文、数学、外语三科各占150分,选考科目成绩采用“赋分制”,即原始分数不直接用,而是按照学生分数在本科目考试的排名来划分等级并以此打分得到最后得分.根据高考综合改革方案,将每门等级考试科目中考生的原始成绩从高到低分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共8个等级.参照正态分布原则,确定各等级人数所占比例分别为3%,7%,16%,24%,24%,16%,7%,3%.等级考试科目成绩计入考生总成绩时,将
共8个等级.参照正态分布原则,确定各等级人数所占比例分别为3%,7%,16%,24%,24%,16%,7%,3%.等级考试科目成绩计入考生总成绩时,将![]() 至
至![]() 等级内的考生原始成绩,依照等比例转换法则,分别转换到91~100,81~90,71~80,61~70,51~60,41~50,31~40,21~30八个分数区间,得到考生的等级成绩.举例说明:某同学化学学科原始分为65分,该学科
等级内的考生原始成绩,依照等比例转换法则,分别转换到91~100,81~90,71~80,61~70,51~60,41~50,31~40,21~30八个分数区间,得到考生的等级成绩.举例说明:某同学化学学科原始分为65分,该学科![]() 等级的原始分分布区间为58~69,则该同学化学学科的原始成绩属
等级的原始分分布区间为58~69,则该同学化学学科的原始成绩属![]() 等级.而
等级.而![]() 等级的转换分区间为61~70,那么该同学化学学科的转换分计算方法为:设该同学化学学科的转换等级分为
等级的转换分区间为61~70,那么该同学化学学科的转换分计算方法为:设该同学化学学科的转换等级分为![]() ,
,![]() ,求得
,求得![]() .四舍五入后该同学化学学科赋分成绩为67.为给高一学生合理选科提供依据,全省对六个选考科目进行测试,某校高一年级2000人,根据该校高一学生的物理原始成绩制成频率分布直方图(见右图).由频率分布直方图,可以认为该校高一学生的物理原始成绩
.四舍五入后该同学化学学科赋分成绩为67.为给高一学生合理选科提供依据,全省对六个选考科目进行测试,某校高一年级2000人,根据该校高一学生的物理原始成绩制成频率分布直方图(见右图).由频率分布直方图,可以认为该校高一学生的物理原始成绩![]() 服从正态分布
服从正态分布![]() ,用这2000名学生的平均物理成绩
,用这2000名学生的平均物理成绩![]() 作为
作为![]() 的估计值,用这2000名学生的物理成绩的方差
的估计值,用这2000名学生的物理成绩的方差![]() 作为
作为![]() 的估计值.
的估计值.
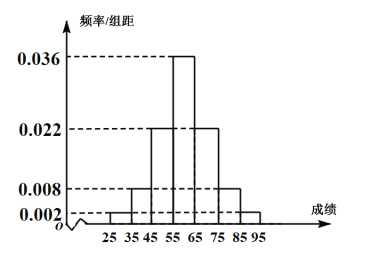
(1)若张明同学在这次考试中的物理原始分为86分,等级为![]() ,其所在原始分分布区间为82~93,求张明转换后的物理成绩(精确到1);按高考改革方案,若从全省考生中随机抽取100人,记
,其所在原始分分布区间为82~93,求张明转换后的物理成绩(精确到1);按高考改革方案,若从全省考生中随机抽取100人,记![]() 表示这100人中等级成绩在区间
表示这100人中等级成绩在区间![]() 内的人数,求
内的人数,求![]() 最有可能的取值(概率最大);
最有可能的取值(概率最大);
(2)①求![]() ,
,![]() (同一组中的数据用该组区间的中点作代表);
(同一组中的数据用该组区间的中点作代表);
②由①中的数据,记该校高一学生的物理原始分高于84分的人数为![]() ,求
,求![]() .
.
附:若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们知道,目前最常见的骰子是六面骰,它是一颗正立方体,上面分别有一到六个洞(或数字),其相对两面之数字和必为七.显然,掷一次六面骰,只能产生六个数之一(正上面).现欲要求你设计一个“十进制骰”,使其掷一次能产生0~9这十个数之一,而且每个数字产生的可能性一样.请问:你能设计出这样的骰子吗?若能,请写出你的设计方案;若不能,写出理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 与圆
与圆![]() 相交于
相交于![]() ,
,![]() 两点,且点
两点,且点![]() 的横坐标为
的横坐标为![]() .
.![]() 是抛物线
是抛物线![]() 的焦点,过焦点的直线
的焦点,过焦点的直线![]() 与抛物线
与抛物线![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() .
.
(1)求抛物线![]() 的方程.
的方程.
(2)过点![]() ,
,![]() 作抛物线
作抛物线![]() 的切线
的切线![]() ,
,![]() ,
,![]() 是
是![]() ,
,![]() 的交点,求证:点
的交点,求证:点![]() 在定直线上.
在定直线上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com