练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】平面ABCD⊥平面ADEF，其中ABCD为矩形，ADEF为梯形，AF∥DE，AF⊥FE，AF=AD=2DE=2，则异面直线EF与BC所成角大小为 ．

    【答案】30°
    【解析】解：延长AD，FE交于Q．
    ∵ABCD是矩形，
    ∴BC∥AD，
    ∴∠AQF是异面直线EF与BC所成的角．
    在梯形ADEF中，由DE∥AF，AF⊥FE，AF=2，DE=1得
    ∠AQF=30°．
    即异面直线EF与BC所成角为30°．
    所以答案是：30°．

    【考点精析】本题主要考查了异面直线及其所成的角的相关知识点，需要掌握异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x|x+a|﹣ lnx．
    （1）当a=0时，讨论函数f（x）的单调性；
    （2）若a＜0，讨论函数f（x）的极值点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列命题：

    ①对立事件一定是互斥事件；②若A，B为两个随机事件，则P(A∪B)＝P(A)＋P(B)；③若事件A，B，C彼此互斥，则P(A)＋P(B)＋P(C)＝1；④若事件A，B满足P(A)＋P(B)＝1，则A与B是对立事件．

    其中正确命题的个数是(　　)

    A. 1 B. 2 C. 3 D. 4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】有下列说法：

    ①在残差图中，残差点比较均匀地落在水平的带状区域内，说明选用的模型比较合适；

    ②用相关指数R2来刻画回归的效果，R2值越大，说明模型的拟合效果越好；

    ③比较两个模型的拟合效果，可以比较残差平方和的大小，残差平方和越小的模型，拟合效果越好．

    ④在研究气温和热茶销售杯数的关系时，若求得相关指数R2≈0.85，则表明气温解释了15％的热茶销售杯数变化.

    其中正确命题的个数是(　　)

    A. 1 B. 2 C. 3 D. 4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义：max{a，b}= ，若实数x，y满足：|x|≤3，|y|≤3，﹣4x≤y≤ x，则max{|3x﹣y|，x+2y}的取值范围是（ ）
    A.[ ，7]
    B.[0，12]
    C.[3， ]
    D.[0，7]

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}满足a1= ，an+1an=2an+1﹣1（n∈N*），令bn=an﹣1．
    （1）求数列{bn}的通项公式；
    （2）令cn= ，求证：c1+c2+…+cn＜n+ ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，已知椭圆的右顶点与上顶点分别为，椭圆的离心率为，且过点.

    （1）求椭圆的标准方程；

    （2）如图，若直线与该椭圆交于两点，直线的斜率互为相反数.

    ①求证：直线的斜率为定值；

    ②若点在第一象限，设与的面积分别为，求的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）满足f（﹣x）=f（x），f（x+8）=f（x），且当x∈（0，4]时f（x）= ，关于x的不等式f2（x）+af（x）＞0在[﹣2016，2016]上有且只有2016个整数解，则实数a的取值范围是（ ）
    A.（﹣ ln6，ln2]
    B.（﹣ln2，﹣ ln6）
    C.（﹣ln2，﹣ ln6]
    D.（﹣ ln6，ln2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图1，平行四边形ABCD中，AB=2AD，∠DAB=60°，M是BC的中点．将△ADM沿DM折起，使面ADM⊥面MBCD，N是CD的中点，图2所示．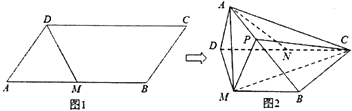

    （Ⅰ）求证：CM⊥平面ADM；
    （Ⅱ）若P是棱AB上的动点，当 为何值时，二面角P﹣MC﹣B的大小为60°．

    查看答案和解析>>

    同步练习册答案