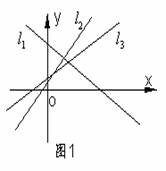
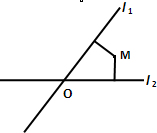
如图1.直线l1.l2.l3的斜率分别为k1.k2.k3. 则必有 A. k1<k3<k2 B. k3<k1<k2 C. k1<k2<k3 D. k3<k2<k1 题目和参考答案——青夏教育精英家教网—

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

科目：高中数学 来源： 题型：

如图，平面中两条直线l₁和l ₂相交于点O，对于平面上任意一点M，若x，y分别是M到直线l ₁和l ₂的距离，则称有序非负实数对（x，y）是点M的“距离坐标”．已知常数p≥0，q≥0，给出下列三个命题：
①若p=q=0，则“距离坐标”为（0，0）的点有且只有1个；
②若pq=0，且p+q≠0，则“距离坐标”为（ p，q）的点有且只有2个；
③若pq≠0则“距离坐标”为（ p，q）的点有且只有3个．
上述命题中，正确的有

①②

．（填上所有正确结论对应的序号）

查看答案和解析>>

科目：高中数学 来源： 题型：

已知二次函数f（x）=3x²-3x直线l₁：x=2和l₂：y=3tx，其中t为常数且0＜＜1．直线l₂与函数f（x）的图象以及直线l₁、l₂与函数f（x）的图象围成的封闭图形如图中阴影所示，设这两个阴影区域的面积之和为S（t）．
（1）求函数S（t）的解析式；
（2）若函数L（t）=S（t）+6t-2，判断L（t）是否存在极值，若存在，求出极值，若不存在，说明理由；
（3）定义函数h（x）=S（x），x∈R若过点A（1，m）（m≠4）可作曲线y=h（x）（x∈R）的三条切线，求实数m的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

如图，三条平行直线l₁，l，l₂把平面分成Ⅰ、Ⅱ、Ⅲ、Ⅳ四个区域（不含边界），且直线l到l₁，l₂的距离相等．点O在直线l上，点A、B在直线
l₁上，P为平面区域内一点，且

OP

=λ1

OA

+λ2

OB

(λ1，λ2∈R)，给出下列四个命题：
（1）若λ₁＞1，λ₂＞1，则点P位于区域Ⅰ；
（2）若点P位于区域Ⅱ，则λ₁+λ₂＞1；
（3）若点P位于区域Ⅲ，则-1＜λ₁+λ₂＜0；
（4）若点P位于区域IV，则λ₁+λ₂＜-1；
则所有正确命题的序号为

（1）（3）（4）

．

查看答案和解析>>

科目：高中数学 来源：不详 题型：填空题

如图，平面中两条直线l₁和l ₂相交于点O，对于平面上任意一点M，若x，y分别是M到直线l ₁和l ₂的距离，则称有序非负实数对（x，y）是点M的“距离坐标”．已知常数p≥0，q≥0，给出下列三个命题：
①若p=q=0，则“距离坐标”为（0，0）的点有且只有1个；
②若pq=0，且p+q≠0，则“距离坐标”为（ p，q）的点有且只有2个；
③若pq≠0则“距离坐标”为（ p，q）的点有且只有3个．
上述命题中，正确的有______．（填上所有正确结论对应的序号）

查看答案和解析>>

科目：高中数学 来源：2012-2013学年福建省厦门六中高一（下）期中数学试卷（解析版） 题型：填空题

如图，平面中两条直线l₁和l ₂相交于点O，对于平面上任意一点M，若x，y分别是M到直线l ₁和l ₂的距离，则称有序非负实数对（x，y）是点M的“距离坐标”．已知常数p≥0，q≥0，给出下列三个命题：
①若p=q=0，则“距离坐标”为（0，0）的点有且只有1个；
②若pq=0，且p+q≠0，则“距离坐标”为（ p，q）的点有且只有2个；
③若pq≠0则“距离坐标”为（ p，q）的点有且只有3个．
上述命题中，正确的有．（填上所有正确结论对应的序号）

查看答案和解析>>

练习册

高中

初中

小学