
分析 因为“p或q”为真命题,“p且q”为假命题,所以p,q中有且仅有一个为真命题.进而可得实数a的取值范围.
解答 解:若p为真命题,则a=0或$\left\{\begin{array}{l}a>0\\{a}^{2}-4a<0\end{array}\right.$.
即0≤a<4;
若q为真命题,则(-1)2-4a≥0,即a≤$\frac{1}{4}$.
因为“p或q”为真命题,“p且q”为假命题,
所以p,q中有且仅有一个为真命题.
若p真q假,则$\frac{1}{4}$<a<4;
若p假q真,则a<0.
综上,实数a的取值范围为(-∞,0)∪($\frac{1}{4}$,4).
点评 本题以命题的真假判断与应用为载体,考查了复合命题,函数的恒成立问题,方程根的存在性及个数判断等知识点,难度中档.


科目:高中数学 来源: 题型:选择题
| A. | 1+i | B. | 1-i | C. | 1+$\frac{i}{2}$ | D. | 1-$\frac{i}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{5}$ | B. | $\frac{7}{5}\sqrt{5}$ | C. | $\frac{17}{5}$ | D. | $\frac{17}{5}\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
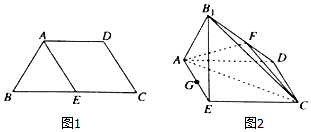 已知四边形ABCD满足AD∥BC,BA=AD=DC=$\frac{1}{2}$BC=a,E是BC的中点,将△BAE沿着AE翻折成△B1AE,使平面B1AE⊥平面ABCD,F,G分别为B1D,AE的中点.
已知四边形ABCD满足AD∥BC,BA=AD=DC=$\frac{1}{2}$BC=a,E是BC的中点,将△BAE沿着AE翻折成△B1AE,使平面B1AE⊥平面ABCD,F,G分别为B1D,AE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$=2-$\frac{1}{{2}^{n}}$ | B. | $\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$<1 | ||
| C. | $\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$=1 | D. | $\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$>1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com