设a、b是不相等的实数，试探求证明不等式(a4＋b4)(a2＋b2)＞(a3＋b3)2的方法．
探究思路：对于不等式的证明比较常见的方法是作差法，即求出不等式两边式子的差，再根据差与零的关系来达到证明不等式的目的．现在我们又学习了向量数量积的坐标表示，因此可以根据不等式结构构造向量利用向量知识来达到证明不等式的目的．
方法一：(a4＋b4)(a2＋b2)－(a3＋b3)2
＝a6＋b6＋a4b2＋a2b4－a6－b6－2a3b3
＝a4b2＋a2b4－2a3b3
＝a2b2(a2－ab)＋a2b2(b2－ab)
＝a2b2(a－b)2．
由于a、b是不相等的实数，则(a4＋b4)(a2＋b2)－(a3＋b3)2＝a2b2(a－b)2＞0，
即(a4＋b4)(a2＋b2)＞(a3＋b3)2．
方法二：设m＝(a2，b2)，n＝(a，b)，
则m·n＝a3＋b3，
又a、b是不相等的实数，则a2b－ab2≠0，
即向量m、n不共线，所以有|m·n|＜|m||n|，即(a4＋b4)(a2＋b2)＞(a3＋b3)2．
学练快车道快乐假期寒假作业系列答案科目：高中数学 来源：2004全国各省市高考模拟试题汇编(天利38套)·数学 题型：044
二次函数f(x)＝ax2＋bx＋c(a、b、c∈R，a≠0)．
(Ⅰ)对于x1、x2∈R，且x1＜x2，f(x1)≠f(x2)，求证：方程f(x)＝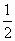
[f(x1)＋f(x2)]有不相等的两实根，且必有一根属于(x1、x2)；
(Ⅱ)若方程f(x)＝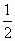
[f(x1)＋f(x2)]在(x1、x2)内的实根为m，且x1、m－
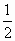、x2成等差数列，设x＝x0是f(x)的对称轴方程．
求证：x0＜m2；
(Ⅲ)若a＞0，f(0)＝1，方程f(x)＝x的两实根为α、β，当|β|＜2，
|α－β|＝2时，求b的取值范围．
查看答案和解析>>
科目：高中数学 来源：成功之路·突破重点线·数学（学生用书） 题型：044
二次函数f(x)＝ax2＋bx＋c(a、b、c∈R，a≠0)．
(Ⅰ)对于x1、x2∈R，且x1＜x2，f(x1)≠f(x2)，求证：方程f(x)＝
[f(x1)＋f(x2)]有不相等的两实根，且必有一根属于(x1、x2)；
(Ⅱ)若方程f(x)＝
[f(x1)＋f(x2)]在(x1、x2)内的实根为m，且x1、m－
、x2成等差数列，设x＝x0是f(x)的对称轴方程．求证：x0＜m2．
(Ⅲ)若a＞0，f(0)＝1，方程f(x)＝x的两实根为α、β，当|β|＜2，|α－β|＝2时，求b的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
A.|x1|＞2且|x2|＞2 B.|x1+x2|＞4
C.|x1+x2|＜4 D.|x1|=4且|x2|=1
查看答案和解析>>
科目：高中数学 来源： 题型：
A.|x1|＞2且|x2|＞2 B.|x1+x2|＞4
C.|x1+x2|＜4 D.|x1|=4且|x2|=1
查看答案和解析>>
科目：高中数学 来源：2013届安徽省高二下学期期中考试理科数学试卷（解析版） 题型：解答题
已知a、b、c是互不相等的非零实数.若用反证法证明三个方程ax2+2bx+c=0，bx2+2cx+a=0，cx2+2ax+b=0至少有一个方程有两个相异实根.
【解析】本试题主要考查了二次方程根的问题的综合运用。运用反证法思想进行证明。
先反设，然后推理论证，最后退出矛盾。证明：假设三个方程中都没有两个相异实根，
则Δ1=4b2－4ac≤0，Δ2=4c2－4ab≤0，Δ3=4a2－4bc≤0
相加有a2－2ab+b2+b2－2bc+c2+c2－2ac+a2≤0，
（a－b）2+（b－c）2+（c－a）2≤0.显然不成立。
证明：假设三个方程中都没有两个相异实根，
则Δ1=4b2－4ac≤0，Δ2=4c2－4ab≤0，Δ3=4a2－4bc≤0.
相加有a2－2ab+b2+b2－2bc+c2+c2－2ac+a2≤0，
（a－b）2+（b－c）2+（c－a）2≤0. ①
由题意a、b、c互不相等，∴①式不能成立.
∴假设不成立，即三个方程中至少有一个方程有两个相异实根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com