
(本题12分)
设命题P:函数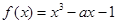 在区间[-1,1]上单调递减;命题q:函数
在区间[-1,1]上单调递减;命题q:函数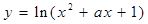 的值域是R.如果命题p或q为真命题,p且q为假命题,求a的取值范围.
的值域是R.如果命题p或q为真命题,p且q为假命题,求a的取值范围.
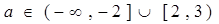 。
。
【解析】
试题分析:p为真命题⇔f'(x)=3x2-a≤0在[-1,1]上恒成立⇔a≥3x2在[-1,1]上恒成立⇔a≥3
q为真命题⇔△=a2-4≥0恒成立⇔a≤-2或a≥2
由题意P和q有且只有一个是真命题p真q假⇔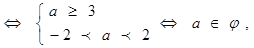
p假q真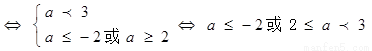 ⇔a≤-2或2≤a<3
⇔a≤-2或2≤a<3
综上所述:a∈(-∞,-2]∪[2,3)
考点:本试题主要考查了命题的真假判断和应用,解题时要注意合理地进行等价转化。
点评:解决该试题的关键由p为真命题,能够推导出a≥3.再由q为真命题,能够推导出a≤-2或a≥2.由题意P和q有且只有一个是真命题,所以p真q假⇔ a≥3,-2< a <2,p假q真⇔a≤-2或2≤a<3.由此能够得到a的取值范围


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源:2013届四川省成都外国语学校高二下学期期中考试数学试卷(解析版) 题型:解答题
(本题满分12分)设命题p:函数 是R上的减函数,命题q:函数f(x)=x2-4x+3在
是R上的减函数,命题q:函数f(x)=x2-4x+3在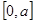 上的值域为[-1,3],若“p且q”为假命题,“p或q”为真命题,求
上的值域为[-1,3],若“p且q”为假命题,“p或q”为真命题,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广西省高三11月月考数学理卷 题型:解答题
(本小题满分12分)
设命题p:函数 是R上的减函数,命题q: 函数
是R上的减函数,命题q: 函数 在
在 的值域是 [-1,3].若“p且q”为假命题。“p或q” 为真命题,求
的值域是 [-1,3].若“p且q”为假命题。“p或q” 为真命题,求 的取值范围
的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com