
【题目】下面推理过程中使用了类比推理方法,其中推理正确的个数是
①“数轴上两点间距离公式为![]() ,平面上两点间距离公式为
,平面上两点间距离公式为![]() ”,类比推出“空间内两点间的距离公式为
”,类比推出“空间内两点间的距离公式为![]() “;
“;
②“代数运算中的完全平方公式![]() ”类比推出“向量中的运算
”类比推出“向量中的运算![]() 仍成立“;
仍成立“;
③“平面内两不重合的直线不平行就相交”类比到空间“空间内两不重合的直线不平行就相交“也成立;
④“圆![]() 上点
上点![]() 处的切线方程为
处的切线方程为![]() ”,类比推出“椭圆
”,类比推出“椭圆![]()
![]() 上点
上点![]() 处的切线方程为
处的切线方程为![]() ”.
”.
A. 1 B. 2 C. 3 D. 4
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某部影片的盈利额(即影片的票房收入与固定成本之差)记为![]() ,观影人数记为
,观影人数记为![]() ,其函数图象如图(1)所示.由于目前该片盈利未达到预期,相关人员提出了两种调整方案,图(2)、图(3)中的实线分别为调整后
,其函数图象如图(1)所示.由于目前该片盈利未达到预期,相关人员提出了两种调整方案,图(2)、图(3)中的实线分别为调整后![]() 与
与![]() 的函数图象.
的函数图象.
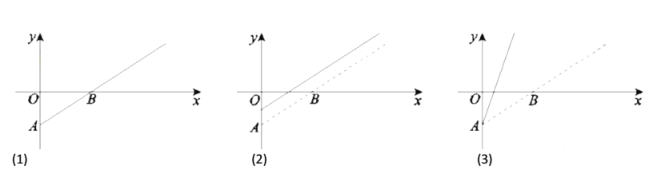
给出下列四种说法:
①图(2)对应的方案是:提高票价,并提高成本;
②图(2)对应的方案是:保持票价不变,并降低成本;
③图(3)对应的方案是:提高票价,并保持成本不变;
④图(3)对应的方案是:提高票价,并降低成本.
其中,正确的说法是____________.(填写所有正确说法的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点,以极轴为
,以极点为原点,以极轴为![]() 轴的正半轴,取相同的单位长度,建立平面直角坐标系,直线
轴的正半轴,取相同的单位长度,建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为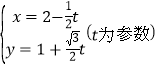 .
.
(1)写出直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 经过伸缩变换
经过伸缩变换![]() 得到曲线
得到曲线![]() ,曲线
,曲线![]() 上任一点为
上任一点为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,函数
,函数![]() .
.
⑴若![]() 的定义域为
的定义域为![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
⑵当![]() ,求函数
,求函数![]() 的最小值
的最小值![]() ;
;
⑶是否存在实数![]() ,使得函数
,使得函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,则说明理由.
的值;若不存在,则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在梯形![]() 中(图1),
中(图1),![]() ,
, ![]() ,
, ![]() ,过
,过![]() 、
、![]() 分别作
分别作![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() 、
、![]() ,已知
,已知![]() ,
, ![]() ,将梯形
,将梯形![]() 沿
沿![]() 、
、![]() 同侧折起,使得
同侧折起,使得![]() ,
, ![]() ,得空间几何体
,得空间几何体![]() (图2).
(图2).
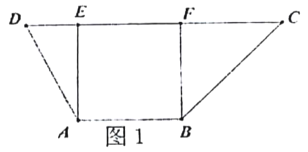
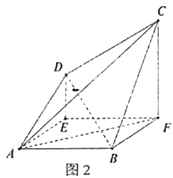
(1)证明: ![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】底面为菱形且侧棱垂直于底面的四棱柱![]() 中,
中, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点,过点
的中点,过点![]() ,
, ![]() ,
, ![]() ,
, ![]() 的平面截直四棱柱
的平面截直四棱柱![]() ,得到平面四边形
,得到平面四边形![]() ,
, ![]() 为
为![]() 的中点,且
的中点,且![]() ,当截面的面积取最大值时,
,当截面的面积取最大值时, ![]() 的值为( )
的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】=2sin(ωx+φ),x∈R,其中ω>0,﹣π<φ≤π.若函数f(x)的最小正周期为6π,且当x=![]() 时,f(x)取得最大值,则( )
时,f(x)取得最大值,则( )
A. f(x)在区间[﹣2π,0]上是增函数B. f(x)在区间[﹣3π,﹣π]上是增函数
C. f(x)在区间[3π,5π]上是减函数D. f(x)在区间[4π,6π]上是减函数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com